题目内容
6．已知M（1）=-2，M（2）=（-2）×（-2），M（3）=（-2）×（-2）×（-2），…，$\underset{\underbrace{M（n）=（-2）×（-2）×…（-2）}}{n个-2相乘}$．（1）计算：M（5）+M（6）
（2）求2M（2016）+M（2017）的值．
（3）猜想2M（n）与M（n+1）的关系并说明理由．
分析 （1）根据$\underset{\underbrace{M（n）=（-2）×（-2）×…（-2）}}{n个-2相乘}$，可得M（5），M（6），根据有理数的加法，可得答案；
（2）根据乘方的意义，可得M（2016），M（2017），根据有理数的加法，可得答案；
（3）根据乘方的意义，可得M（n），M（n+1），根据有理数的加法，可得答案．
解答 解：（1）M（5）+M（6）=（-2）5+（-2）6=-32+64=32；
（2）2M（2016）+M（2017）=2×（-2）2016+（-2）2017=2×22016-22017=22017-22017=0；
（3）∵2M（n）+M（n+1）=-（-2）×（-2）n+（-2）n+1=-（-2）n+1+（-2）n+1=0，
∴2M（n）与M（n+1）互为相反数．
点评 本题考查了规律型：数字的变化类，同底数幂的乘法，利用了同底数幂的乘法，相反数的性质：互为相反数的和为零．
练习册系列答案
阅读快车系列答案
相关题目
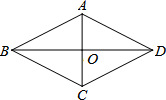如图，菱形ABCD中，对角线AC、BD相交于点O．AC=3$\sqrt{2}$+2$\sqrt{3}$，BD=3$\sqrt{2}$-2$\sqrt{3}$．求：菱形ABCD的面积和周长．
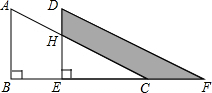如图，将Rt△ABC沿射线BC方向平移得到△DEF，已知AB=16cm，BE=10cm，DH=6cm，则图中阴影部分的面积为130cm2．
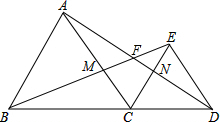如图，B、C、D在同一直线上，△ABC和△DCE都是等边三角形，且在直线BD的同侧，BE交AD于F，BE交AC于M，AD交CE于N．
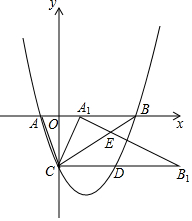如图，已知抛物线与y轴交于点C（0，-3），与x轴交于点A（-1，0）B（4，0），将△ABC绕点C顺时针旋转α得△A1B1C（点A，B的对应点分别为点A1，B1），CB1交抛物线于点D，射线A1B1与射线BC交于点E．