题目内容
15.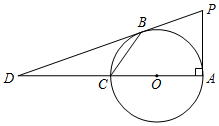 如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.
如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.
分析 连接OB、OP,如图,利用切线的性质得OB⊥PD,利用切线的判定得到PA为⊙O的切线,则利用切线长定理得到PA=PB,设圆的半径为r,利用$\frac{DC}{DO}$=$\frac{2}{3}$得到DC=2r,OD=3r,利用勾股定理得到BD=2$\sqrt{2}$r,接着由$\frac{DB}{DP}$=$\frac{2}{3}$得到PB=$\sqrt{2}$r,所以AB=$\sqrt{2}$r,再证明△DBC∽△DPO得到∠BCD=∠POD,则判定BC∥PO得到∠POA=∠ACB,然后利用余弦的定义求出cos∠AOP即可得到cos∠BCA的值.
解答 解:连接OB、OP,如图,
∵PB为切线,
∴OB⊥PD,
∵PA⊥AD,
∴PA为⊙O的切线,
∴PA=PB,
设圆的半径为r,
∵$\frac{DC}{DO}$=$\frac{2}{3}$,
∴DC=2r,OD=3r,
在Rt△BOD中,BD=$\sqrt{(3r)^{2}-{r}^{2}}$=2$\sqrt{2}$r,
∵$\frac{DB}{DP}$=$\frac{2}{3}$,
∴PB=$\sqrt{2}$r,
∴AB=$\sqrt{2}$r,
∵$\frac{DB}{DP}$=$\frac{DC}{DO}$,
而∠BDC=∠PDO,
∴△DBC∽△DPO,
∴∠BCD=∠POD,
∴BC∥PO,
∴∠POA=∠ACB,
在Rt△OPA中,OP=$\sqrt{(\sqrt{2}r)^{2}+{r}^{2}}$=$\sqrt{3}$r,
cos∠AOP=$\frac{OA}{OP}$=$\frac{r}{\sqrt{3}r}$=$\frac{\sqrt{3}}{3}$,
∴cos∠BCA=$\frac{\sqrt{3}}{3}$.
故答案为$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;再运用相似三角形的性质时主要利用相似比计算线段的长.也考查了切线的性质.

| A. | a=b | B. | b=c | C. | a=c | D. | a=b=c |
 如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )
如图,在△ABC中,∠B=90°,AB=21,BC=20,有一个半径为10的圆分别与AB、BC相切,则此圆的圆心是( )| A. | AB边的中垂线与BC中垂线的交点 | B. | ∠B的平分线与AB的交点 | ||
| C. | ∠B的平分线与AB中垂线的交点 | D. | ∠B的平分线与BC中垂线的交点 |
 如图,菱形花坛ABCD的边长为10m,∠BAD=120°,沿着菱形的对角线修建了两条小路AC和BD
如图,菱形花坛ABCD的边长为10m,∠BAD=120°,沿着菱形的对角线修建了两条小路AC和BD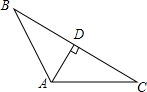 如图,在△ABC中,已知:∠CAB=120°,AB=3,AC=5,AD⊥BC于D,试求:
如图,在△ABC中,已知:∠CAB=120°,AB=3,AC=5,AD⊥BC于D,试求: