题目内容
20.已知直线l1与直线l2:y=$\frac{1}{3}$x+3平行,直线l1与x轴的交点的坐标为A(2,0),求:(1)直线l1的表达式.
(2)直线l1与坐标轴围成的三角形的面积.
分析 (1)由直线l1与直线l2:y=$\frac{1}{3}$x+3平行易得k=$\frac{1}{3}$,设l1解析式为y=$\frac{1}{3}$x+b,将A(2,0)代入解析式,解得b,可得l1表达式;
(2)令x=0,可得直线l1与y轴的交点,利用三角形的面积公式可得结果.
解答 解:(1)∵直线l1与直线l2:y=$\frac{1}{3}$x+3平行,
∴设l1解析式为y=$\frac{1}{3}$x+b,
∵直线l1与x轴的交点的坐标为A(2,0),
∴0=$\frac{1}{3}×2+b$
解得,b=$-\frac{2}{3}$,
∴直线l1的表达式为:y=$\frac{1}{3}x-\frac{2}{3}$;
(2)设直线l1与x轴、y轴的交点的坐标分别为A,B,
令x=0,可得y=$\frac{1}{3}×0-\frac{2}{3}$=$-\frac{2}{3}$,
则B点坐标为(0,-$\frac{2}{3}$)
S△AOB=$\frac{1}{2}$•|OA|•|OB|=$\frac{1}{2}×$2×$\frac{2}{3}$=$\frac{2}{3}$.
直线l1与坐标轴围成的三角形的面积为:$\frac{2}{3}$.
点评 本题主要考查了两直线相交与平行问题,求得直线与两坐标轴的交点坐标是解答此题的关键.

练习册系列答案
相关题目
11.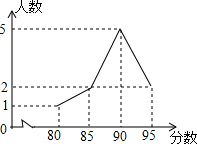 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,则这10名学生成绩的平均数是( )| A. | 88 | B. | 89 | C. | 90 | D. | 91 |
8.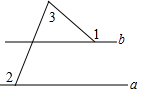 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )
 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )| A. | 180° | B. | 150° | C. | 135° | D. | 90° |
5.九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
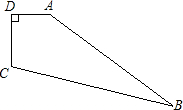 如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.
如图,在四边形ABCD中,∠D=90°,AD=3,DC=4,AB=12,BC=13.求四边形ABCD的面积.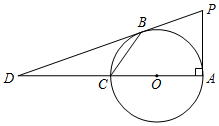 如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$.
如图所示,AC为⊙O的直径,PA⊥AC于点A,过点P作⊙O 的切线PB交AC于点D,连接BC,且$\frac{DB}{DP}$=$\frac{DC}{DO}$=$\frac{2}{3}$,则cos∠BCA的值等于$\frac{\sqrt{3}}{3}$. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是3.
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是3.