题目内容
8.已知x,y,z为实数,且2x-3y+z=3,则x2+(y-1)2+z2的最小值为$\frac{18}{7}$.分析 由条件可得z=3-2x+3y,x2+(y-1)2+z2=x2+(y-1)2+(3-2x+3y)2=5[x-1.2(y+1)]2+2.8(y+$\frac{2}{7}$)2+$\frac{18}{7}$≥$\frac{18}{7}$,据此可得.
解答 解:由2x-3y+z=3得z=3-2x+3y,
x2+(y-1)2+z2
=x2+(y-1)2+(3-2x+3y)2
=5x2-12x(y+1)+9(y+1)2+(y-1)2
=5[x-1.2(y+1)]2+1.8(y+1)2+(y-1)2
=5[x-1.2(y+1)]2+2.8(y+1)2+1.6y+2.8
=5[x-1.2(y+1)]2+2.8[y2+$\frac{1.6}{2.8}$y+($\frac{0.8}{2.8}$)2]+2.8-$\frac{0.{8}^{2}}{2.8}$
=5[x-1.2(y+1)]2+2.8(y+$\frac{2}{7}$)2+$\frac{18}{7}$≥$\frac{18}{7}$,
∴x2+(y-1)2+z2的最小值为$\frac{18}{7}$,
故答案为:$\frac{18}{7}$.
点评 本题主要考查配方法的应用,注意运用配方法和非负数的思想是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
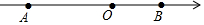 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.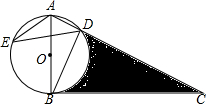 如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB. 如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.
如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是48.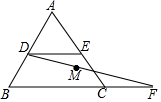 如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.
如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.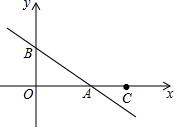 如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).
如图,直线y=-$\frac{2}{3}$x+m分别交x轴、y轴于A、B两点,已知点C(6,0).