题目内容
17.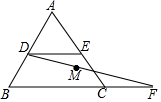 如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.
如图,已知等边△ABC的边长为6,D、E分别是AB、AC边上的动点,DE∥BC,将线段CE绕C点顺时针旋转120°,得到线段CF,连接DF,则当点D在AB边上从A运动到B的过程中,DF的中点M运动的路径长为3$\sqrt{3}$.
分析 如图,取BC中点N,连接NM,将线段BD绕B点逆时针旋转120°,得到线段BG,连接DG.点M的运动轨迹为线段MN,当点D与A重合时,易知DG=2•AB•cos30°=6$\sqrt{3}$,推出MN=$\frac{1}{2}$DG=3$\sqrt{3}$.
解答 解:如图,取BC中点N,连接NM,将线段BD绕B点逆时针旋转120°,得到线段BG,连接DG.
∵△ABD是等边三角形,DE∥BC,
∴∠ADE=∠ABC=60°,∠AED=∠ACB=60°,
∴∠ADE=∠AED,
∴AD=AE,BD=EC,
∵BD=BG,CE=CF,BN=CN,
∴NG=FN,∵DM=MF,
∴MN=$\frac{1}{2}$DG,MN∥DG,∠MNF=∠G=30°,
易知点M的运动轨迹为线段MN,当点D与A重合时,易知DG=2•AB•cos30°=6$\sqrt{3}$,
∴MN=$\frac{1}{2}$DG=3$\sqrt{3}$,
故答案为3$\sqrt{3}$.
点评 本题考查等边三角形的性质、旋转变换、三角形的中位线定理、轨迹等知识,解题的关键是正确寻找点M的运动轨迹,属于中考填空题中的压轴题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完100只节能灯后,该商场获利多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
(2)全部售完100只节能灯后,该商场获利多少元?
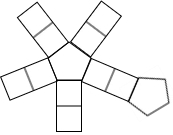 “磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
“磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )


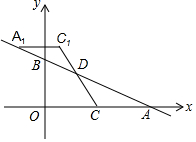 如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
如图,一次函数y=-$\frac{1}{2}$x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.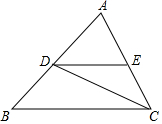 已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件
已知如图,在△ABC中,2∠B=∠ACB,给出下列3个条件