题目内容
20.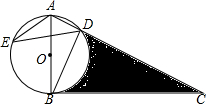 如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB.
如图,在△ABC中,以AB为直径的⊙O交AC于点D,点E在⊙O上,且$\widehat{AE}$=$\widehat{BE}$,连接BD,∠CBD=∠CAB.(1)求证:BC是⊙O的切线;
(2)若sin∠AED=$\frac{1}{2}$,AE=3$\sqrt{2}$,求BC的长及图中阴影的面积.
分析 (1)欲证明BC是⊙O的切线,只要证明AB⊥BC即可;
(2)首先证明∠C=30°,∠BOD=120°,求出BD、CD、BC,根据S阴=S△BDC-(S扇形-S△OBD)计算即可;
解答 (1)证明:∵AB是直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠]BAD=∠DBC,
∴∠ABD+∠DBC=90°,
∴∠ABC=90°,即AB⊥BC,
∴BC是⊙O的切线.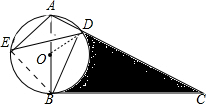
(2)解:连接EB,OD.
∵AB是直径,
∴∠AEB=90°,
∵$\widehat{AE}$=$\widehat{EB}$,
∴AE=EB=3$\sqrt{2}$,
∴AB=$\sqrt{2}$AE=6,
∵∠AED=∠ABD,
∴sin∠ABD=sin∠AED=$\frac{1}{2}$=$\frac{AD}{AB}$,
∴AD=3,BD=3$\sqrt{3}$,∠ABD=30°,
∴∠DBC=60°,∠C=30°,
∴CD=$\sqrt{3}$BD=9,BC=2BD=6$\sqrt{3}$,
∴S阴=S△BDC-(S扇形-S△OBD)
=$\frac{1}{2}$•3$\sqrt{3}$•9-($\frac{120•π•{3}^{2}}{360}$-$\frac{1}{2}$•3$\sqrt{3}$•$\frac{3}{2}$)
=$\frac{45\sqrt{3}}{4}$-3π.
点评 本题考查切线的判定和性质、解直角三角形、锐角三角函数、扇形的面积公式等知识,解题的关键是学会添加常用辅助线,学会用转化的扇形思考问题,属于中考常考题型.

练习册系列答案
相关题目
11.某商场用3300元购进节能灯100只,这两种节能灯的进价、售价如表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完100只节能灯后,该商场获利多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
(2)全部售完100只节能灯后,该商场获利多少元?
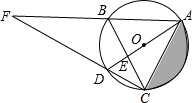 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题: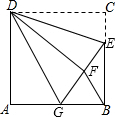 如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号)
如图,正方形ABCD的边长为12,点E在边BC上,且BE=2CE.将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连结DG,BF.下列结论:①△DAG≌△DFG;②DG∥BF;③EG=10;④S△BEF=9.6.其中所有正确结论的序号是①②③④(填序号) ,则其代表的算式是(-65)2-5,结果是4220.
,则其代表的算式是(-65)2-5,结果是4220.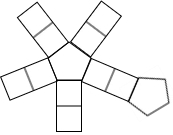 “磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )
“磁力健构片”通过磁铁连接重心,可以轻松制作成球体、锥体、正方体等百种造型,立体提拉魔幻成型,直观立体,是全面开发脑力的益智玩具.如图所示的平面图形经过立体提拉后,会成型为( )