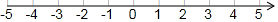题目内容
17. 如图,已知C为⊙O的弦AB上一点,CD⊥OC交⊙O于D,AC=8,BC=4,则CD的长是4$\sqrt{2}$.
如图,已知C为⊙O的弦AB上一点,CD⊥OC交⊙O于D,AC=8,BC=4,则CD的长是4$\sqrt{2}$.
分析 延长DC交⊙O于点E,连接AE,DB,根据相似三角形的判定定理得出△ACE∽△DCB,再由相似三角形的对应边成比例得出CD•CE=AC•CB.再由垂径定理即可得出结论.
解答  解:延长DC交⊙O于点E,连接AE,DB,
解:延长DC交⊙O于点E,连接AE,DB,
∵∠A=∠D,∠E=∠B,
∴△ACE∽△DCB,
∴$\frac{AC}{CD}$=$\frac{CE}{CB}$,
∴CD•CE=AC•CB.
∵OC⊥CD,
∴CE=CD,
∴CD2=8×4=32,
∴CD=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
7.满足-$\sqrt{2}$<x<$\sqrt{5}$的整数x是( )
| A. | -1,0,1,2 | B. | -2,-1,0,1 | C. | -1,1,2,3 | D. | 0,1,2,3 |
 如图,已知A、B、C、D是⊙O上的四点,若∠BOD=100°,则∠C=130°.
如图,已知A、B、C、D是⊙O上的四点,若∠BOD=100°,则∠C=130°.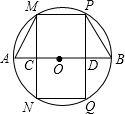 如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,
如图,AB是⊙O直径,C、D是AB上两点,MC⊥AB交⊙O于M、N,PD⊥AB交⊙O于P、Q,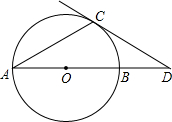 如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.