题目内容
9.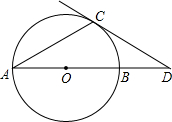 如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.(1)求证:DC是⊙O的切线.
(2)若BD=1cm,求AC的长.
分析 (1)连接OC、BC,如图,利用圆周角定理得到∠ACB=90°,则可计算出∠COB=60°,于是可判断△OBC 是等边三角形,则∠OCB=∠OBC=60°,再利用等腰三角形的性质和三角形外角性质计算出∠BCD=30°,从而得到∠OCD=90°,然后根据切线的判定定理可得到结论;
(2)利用等边三角形的性质得OB=BD=BC=1,然后在Rt△ABC中利用含30度的直角三角形三边的关系可计算出AC.
解答 (1)证明:连接OC、BC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵OA=OC,
∴∠OCA=∠A=30°,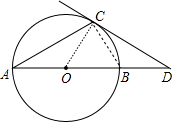
∴∠COB=∠A+∠OCA=60°,
∵OC=OB,
∴△OBC 是等边三角形,
∴∠OCB=∠OBC=60°,
又∵BD=OB,
∴∠BDC=∠BCD,
而∠OBC=∠BDC+∠BCD,
∴∠BCD=30°,
∴∠OCD=∠OCB+∠BCD=90°,
∴OC⊥CD,
∴DC是⊙O的切线;
(2)解:OB=BD=BC=1,
在Rt△ABC中,∴∠A=30°,
∴AC=$\sqrt{3}$BC=$\sqrt{3}$cm.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
1.下列各数$\frac{π}{2}$,0,$\sqrt{9}$,0.2$\stackrel{•}{3}$,$\frac{22}{7}$,0.10010001,$\sqrt{2}$中无理数个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出20件,但最低单价应高于购进的价格,并且已知第二月后T恤还有剩余;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表
(2)如果批发商希望通过销售这批T恤获利12000元,那么第二个月的单价应是多少元?
(1)填表
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(件) | 200 | 200+20x | 400-20x |
 如图,已知C为⊙O的弦AB上一点,CD⊥OC交⊙O于D,AC=8,BC=4,则CD的长是4$\sqrt{2}$.
如图,已知C为⊙O的弦AB上一点,CD⊥OC交⊙O于D,AC=8,BC=4,则CD的长是4$\sqrt{2}$. 二次函数y=ax2+bx+c的图象如图,点(1,0)在函数图象上,那么abc、2a+b、a+b+c、a-b+c这四个代数式中,值大于或等于零的数有( )
二次函数y=ax2+bx+c的图象如图,点(1,0)在函数图象上,那么abc、2a+b、a+b+c、a-b+c这四个代数式中,值大于或等于零的数有( )