题目内容
7．满足-$\sqrt{2}$＜x＜$\sqrt{5}$的整数x是（ ）| A． | -1，0，1，2 | B． | -2，-1，0，1 | C． | -1，1，2，3 | D． | 0，1，2，3 |
分析 先求出-$\sqrt{2}$、$\sqrt{5}$的近似值，再根据x的取值范围找出x的整数解即可．
解答 解：因为-$\sqrt{2}$≈-1.414，$\sqrt{5}$≈2.236，
所以满足-$\sqrt{2}$＜x＜$\sqrt{5}$的整数x是-1，0，1，2．
故选A．
点评 此题主要考查了实数的大小的比较，解题关键是首先正确估计无理数的大小，然后再进一步找出满足范围的整数．
练习册系列答案
相关题目
如图，已知C为⊙O的弦AB上一点，CD⊥OC交⊙O于D，AC=8，BC=4，则CD的长是4$\sqrt{2}$．
18．某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出20件，但最低单价应高于购进的价格，并且已知第二月后T恤还有剩余；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓时单价为40元．设第二个月单价降低x元．
（1）填表
（2）如果批发商希望通过销售这批T恤获利12000元，那么第二个月的单价应是多少元？
（1）填表
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价（元） | 80 | 80-x | 40 |
| 销售量（件） | 200 | 200+20x | 400-20x |
16．下列从左边到右边的变形，是因式分解的是（ ）
| A． | （3-x）（3+x）=9-x2 | B． | m2-n2=（m-n）（m+n） | ||
| C． | （y+1）（y-3）=-（3-y）（y+1） | D． | 4yz-2y2z+z=2y（2z-yz）+z |
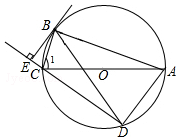如图，⊙O是△ABC的外接圆，AC为直径，弦BD=BA，过点B作⊙O的切线交DC的延长线于点E．