题目内容
2.若关于x的方程x2+(m+1)x+$\frac{1}{2}$=0的一个实数根的倒数恰是它本身,则m的值是( )| A. | -$\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{5}{2}$或$\frac{1}{2}$ | D. | 1 |
分析 由根与系数的关系可得:x1+x2=-(m+1),x1•x2=$\frac{1}{2}$,又知一个实数根的倒数恰是它本身,则该实根为1或-1,然后把±1分别代入两根之和的形式中就可以求出m的值.
解答 解:由根与系数的关系可得:
x1+x2=-(m+1),x1•x2=$\frac{1}{2}$,
又知一个实数根的倒数恰是它本身,
则该实根为1或-1,
若是1时,即1+x2=-(m+1),而x2=$\frac{1}{2}$,解得m=-$\frac{5}{2}$;
若是-1时,则m=$\frac{1}{2}$.
故选:C.
点评 本题考查了一元二次方程的解的定义和一元二次方程根与系数的关系.解此类题目要会把代数式变形为两根之积或两根之和的形式,代入数值计算即可.

练习册系列答案
相关题目
14.已知x2-3x-4=0,则代数式$\frac{x}{{{x^2}-x-4}}$的值是( )
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
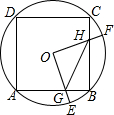 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: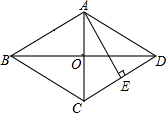 如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.
如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$. 如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.
如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°. 如图是由4个完全相同的小正方体组成的立体图形,则它的俯视图是( )
如图是由4个完全相同的小正方体组成的立体图形,则它的俯视图是( )



 一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):