题目内容
5.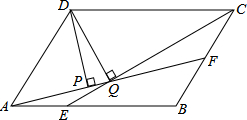 如图,平行四边形ABCD中,AB=3,BC=2,∠DAB=60°,E在AB上,且AE=$\frac{1}{2}$EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为2$\sqrt{3}$:$\sqrt{13}$.
如图,平行四边形ABCD中,AB=3,BC=2,∠DAB=60°,E在AB上,且AE=$\frac{1}{2}$EB,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ的值为2$\sqrt{3}$:$\sqrt{13}$.
分析 连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,根据三角形的面积和平行四边形的面积得出S△DEC=S△DFA=$\frac{1}{2}$S平行四边形ABCD,求出AF×DP=CE×DQ,求出BF=1,BE=2,BN=$\frac{1}{2}$,BM=a,FN=$\frac{\sqrt{3}}{2}$,CM=$\sqrt{3}$,求出AF=$\sqrt{13}$,CE=2$\sqrt{3}$,代入求出即可.
解答  解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
∵根据三角形的面积和平行四边形的面积得:S△DEC=S△DFA=$\frac{1}{2}$S平行四边形ABCD,
即$\frac{1}{2}$AF×DP=$\frac{1}{2}$CE×DQ,
∴AF×DP=CE×DQ,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠DAB=60°,
∴∠CBN=∠DAB=60°,
∴∠BFN=∠MCB=30°,
∵AB=3,BC=2,
∴设AB=3a,BC=2a,
∵AE:EB=1:2,F是BC的中点,
∴BF=1,BE=2,
BN=$\frac{1}{2}$,BM=1,
由勾股定理得:FN=$\frac{\sqrt{3}}{2}$,CM=$\sqrt{3}$,
AF=$\sqrt{(3+\frac{1}{2})^{2}+({\frac{\sqrt{3}}{2})}^{2}}$=$\sqrt{13}$,CE=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
∴$\sqrt{13}$•DP=2$\sqrt{3}$•DQ
∴DP:DQ=2$\sqrt{3}$:$\sqrt{13}$,
故答案为:2$\sqrt{3}$:$\sqrt{13}$.
点评 本题考查了平行四边形面积,勾股定理,三角形的面积,含30度角的直角三角形等知识点的应用,关键是求出AF×DP=CE×DQ和求出AF、CE的值.

| A. | 100(1+x) | B. | 100(1+x)2 | C. | 100(1+x2) | D. | 100(1+2x) |
 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(3,0)和B(0,4),则图象过点C的反比例函数解析式为( )| A. | $y=\frac{20}{x}$ | B. | $y=-\frac{20}{x}$ | C. | $y=\frac{12}{x}$ | D. | $y=-\frac{12}{x}$ |
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
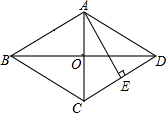 如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.
如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$. 如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.
如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=65°.