题目内容
13.对于一个无理数m,我们把不超过m的最大整数叫做m的整数部分,把m减去整数部分的差叫做m的小数部分,设x=$\sqrt{2}$+1,a是x的小数部分,b是-x的小数部分,求a3+b3+3ab的值.分析 根据是x的小数部分,b是-x的小数部分,分别求出a和b的值,然后把a3+b3+3ab分解因式,代值计算.
解答 解:∵2<$\sqrt{2}$+1<3,
∴a=x-2=$\sqrt{2}$-1.
又∵-x=-$\sqrt{2}$-1,
∵-3<-$\sqrt{2}$-1<-2,
∴b=-$\sqrt{2}$-1+3=2-$\sqrt{2}$.
∴a+b=1,
∴a3+b3+3ab
=(a+b)(a2-ab+b2)+3ab
=(a2-ab+b2)+3ab
=a2+2ab+b2
=(a+b)2
=1.
故a3+b3+3ab的值为1.
点评 本题主要考查立方公式的知识点,解答本题的关键是a+b的值,本题难度不大.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2$\sqrt{3}$,BC=2.求⊙O的半径.
 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;
(2)已知PA=2$\sqrt{3}$,BC=2.求⊙O的半径.
5.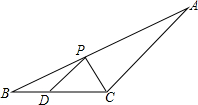 如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
 如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{7}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
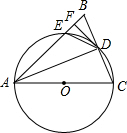 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.