题目内容
5.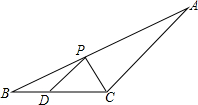 如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{7}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 先确定DC′=DP+PC′=DP+CP的值最小,然后根据勾股定理计算.
解答 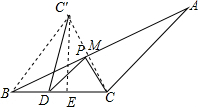 解:过点C作CM⊥AB于M,延长CM到C′,使MC′=MC,连接DC′,交AB于P,连接CP,
解:过点C作CM⊥AB于M,延长CM到C′,使MC′=MC,连接DC′,交AB于P,连接CP,
此时DP+CP=DP+PC′=DC′的值最小.
∵∠ABC=30°,
∴CM=$\frac{1}{2}$BC,∠BCC′=60°,
∴CC′=2CM=BC,
∴△BCC′是等边三角形,
作C′E⊥BC于E,
∴BE=EC=$\frac{1}{2}$BC=3,C′E=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$,
∵BD=2,
∴DE=1,
根据勾股定理可得DC′=$\sqrt{C′{E}^{2}+D{E}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{1}^{2}}$=2$\sqrt{7}$.
故选A.
点评 此题考查了线路最短的问题,确定动点E何位置时,使PC+PD的值最小是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
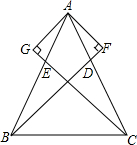 已知,如图,在△ABC中,AB=AC,BD、CE分别为AC、AB边上的中线,AF⊥BD于F,AG⊥CE于G.求证:AF=AG.
已知,如图,在△ABC中,AB=AC,BD、CE分别为AC、AB边上的中线,AF⊥BD于F,AG⊥CE于G.求证:AF=AG.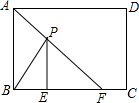 如图,在矩形ABCD中,AB=4cm,AD=5cm,点E在BC边上,且BE=1cm,AF平分∠BAD,图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为5cm.
如图,在矩形ABCD中,AB=4cm,AD=5cm,点E在BC边上,且BE=1cm,AF平分∠BAD,图中P为AF上任意一点,若P为AF上任意一动点,请确定一点P,连接BP、EP,则BP+EP的最小值为5cm. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,E为AC的中点,ED、CB的延长线交于点F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,E为AC的中点,ED、CB的延长线交于点F.