题目内容
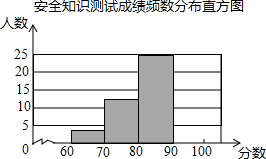 某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).
某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).安全知识测试成绩频数分布表
| 组别 | 成绩x(分数) | 组中值 | 频数(人数) |
| 1 | 90≤x<100 | 95 | 10 |
| 2 | 80≤x<90 | 85 | 25 |
| 3 | 70≤x<80 | 75 | 12 |
| 4 | 60≤x<70 | 65 | 3 |
(2)这个样本数据的中位数在第
(3)若将各组的组中值视为该组的平均成绩,则此次测试的平均成绩为
(4)若将90分以上(含90分)定为“优秀”等级,则该县10000名初中生中,获“优秀”等级的学生约为
考点:频数(率)分布直方图,用样本估计总体,频数(率)分布表,加权平均数,中位数
专题:
分析:(1)确定第四小组的频数后即可补全频数分布直方图;
(2)根据总人数确定中位数是那两个数据的平均数,然后结合各小组的频数求解即可;
(3)用加权平均数计算平均成绩即可;
(4)首先确定优秀率,然后确定优秀的人数.
(2)根据总人数确定中位数是那两个数据的平均数,然后结合各小组的频数求解即可;
(3)用加权平均数计算平均成绩即可;
(4)首先确定优秀率,然后确定优秀的人数.
解答:解:(1)完成图形如下:

(2)∵共50个人,
∴中位数应该是第25和第26个数据的平均数,
∵第25和第26个数据均落在第2小组,
∴中位数落在第2小组;
(3)平均数=
=83.4;
(4)该县10000名初中生中,获“优秀”等级的学生约为10000×
=2000人,
故答案为:2,83,2000.

(2)∵共50个人,
∴中位数应该是第25和第26个数据的平均数,
∵第25和第26个数据均落在第2小组,
∴中位数落在第2小组;
(3)平均数=
| 65×3+75×12+85×25+95×10 |
| 50 |
(4)该县10000名初中生中,获“优秀”等级的学生约为10000×
| 10 |
| 50 |
故答案为:2,83,2000.
点评:本题考查了频数分布表及频率分布直方图的知识,解题的关键是能够了解频率、频数及样本总数的关系,难度不大.

练习册系列答案
相关题目
若x≠y,则下列不能成立的等式是( )
| A、(x-y)2 =(y-x)2 |
| B、(x-y)3 =-(y-x)3 |
| C、(x+y)2 =(-x-y)2 |
| D、(x+y)2 =(-x+y)2 |
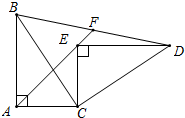 如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.
如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD. 在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.
在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.