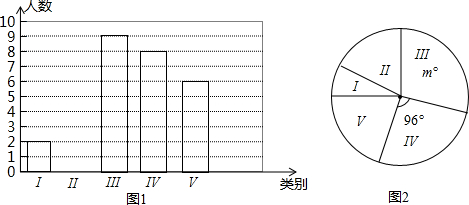
题目内容
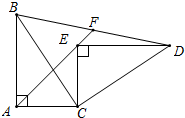 如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.
如图所示,Rt△ABC≌Rt△CED,∠BAC=∠CED=90°,延长AE到BD交与点F,求证:BF=FD.考点:全等三角形的判定与性质
专题:证明题
分析:作DG∥AB交AF的延长线于G,易证∠BAF=∠DEG,即可求得∠DGF=∠DEG,可得DG=DE,易证DE=BA,即可求得AB=DG,即可证明△BAF≌△DGF,即可解题.
解答:证明:作DG∥AB交AF的延长线于G,
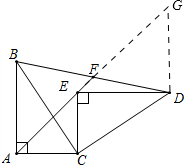
∵∠BAF+∠CAE=90°,∠DEG+∠CEA=90°,∠CAE=∠CEA,
∴∠BAF=∠DEG,
∵∠BAF=∠DGF,
∴∠DGF=∠DEG,
∴DG=DE,
∵Rt△ABC≌Rt△CED,
∴DE=BA,
∴AB=DG,
在△BAF和△DGF中,
,
∴△BAF≌△DGF(AAS),
∴BF=DF.

∵∠BAF+∠CAE=90°,∠DEG+∠CEA=90°,∠CAE=∠CEA,
∴∠BAF=∠DEG,
∵∠BAF=∠DGF,
∴∠DGF=∠DEG,
∴DG=DE,
∵Rt△ABC≌Rt△CED,
∴DE=BA,
∴AB=DG,
在△BAF和△DGF中,
|
∴△BAF≌△DGF(AAS),
∴BF=DF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BAF≌△DGF是解题的关键.

练习册系列答案
相关题目
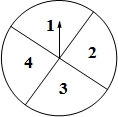 如图,是一个可以自由转动的转盘,转盘被平均分成四个相同的扇形,分别写有1、2、3、4四个数字,指针位置固定,转动转盘后任其自由停止(指针指向边界时重转),现转动转盘两次,请用画树形图法或列表法求出指针指向相同数字的概率.
如图,是一个可以自由转动的转盘,转盘被平均分成四个相同的扇形,分别写有1、2、3、4四个数字,指针位置固定,转动转盘后任其自由停止(指针指向边界时重转),现转动转盘两次,请用画树形图法或列表法求出指针指向相同数字的概率. 如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证:
如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证: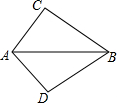 如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件
如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件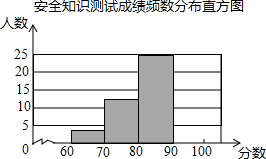 某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).
某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).