题目内容
抛物线y=(x-5)2的开口,对称轴是 ,顶点坐标是 ,它可以看做是由抛物线y=x2向 平移 个单位长度得到的.抛物线 向右平移3个单位长度即得到抛物线y=2(x-1)2.
考点:二次函数图象与几何变换
专题:
分析:确定出y=(x-5)2的顶点坐标,再根据顶点的变化确定出平移方法,然后根据二次函数的性质分别写出开口方向,对称轴即可.
解答:解:抛物线y=(x-5)2的开口向上,对称轴是直线x=5,顶点坐标是(5,0),它可以看作是由抛物线y=x2向右平移5个单位长度得到的.
抛物线y=2(x+2)2向右平移3个单位长度即得到抛物线y=2(x-1)2.
故答案为:向上,x=5,(5,0),右,5,y=2(x+2)2.
抛物线y=2(x+2)2向右平移3个单位长度即得到抛物线y=2(x-1)2.
故答案为:向上,x=5,(5,0),右,5,y=2(x+2)2.
点评:本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.

练习册系列答案
相关题目
世界杯足球赛正在巴西如火如荼地进行,赛前有人预测,巴西国家队夺冠的概率是90%.对他的说法理解正确的是( )
| A、巴西队一定会夺冠 |
| B、巴西队一定不会夺冠 |
| C、巴西队夺冠的可能性很大 |
| D、巴西队夺冠的可能性很小 |
 如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证:
如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证: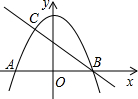 如图,抛物线y=-
如图,抛物线y=-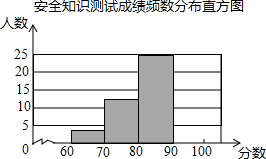 某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).
某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD=
在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD= 如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E.
如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E.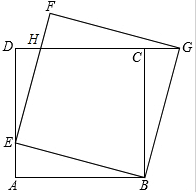 如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.