题目内容
 在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.
在△ABC中,AB=AC,点D在BC边上,且BD=AD,AB+AD=BC,求∠B的度数.考点:等腰三角形的性质
专题:
分析:设∠B=x,易证∠C=∠B=x,∠CAD=∠CDA,根据BD=AD即可求得∠CAD=∠CDA=2x,即可求得x的值,即可解题.
解答:解:设∠B=x,
∵AB=AC,∴∠C=∠B=x,
∵BD=AD,AB+AD=BC,AB=AC,
∴AC=CD,
∴∠CAD=∠CDA,
∵BD=AD,
∴∠BAD=∠B=x,
∴∠CAD=∠CDA=2x,
∵∠CAD+∠CDA+∠C=180°,即5x=180°,
解得:x=36°,
∴∠B=36°.
∵AB=AC,∴∠C=∠B=x,
∵BD=AD,AB+AD=BC,AB=AC,
∴AC=CD,
∴∠CAD=∠CDA,
∵BD=AD,
∴∠BAD=∠B=x,
∴∠CAD=∠CDA=2x,
∵∠CAD+∠CDA+∠C=180°,即5x=180°,
解得:x=36°,
∴∠B=36°.
点评:本题考查了等腰三角形底角相等的性质,考查了三角形内角和为180°的性质,本题中求证∠CAD=∠CDA=2x是解题的关键.

练习册系列答案
相关题目
下列方程中,是关于x的一元二次方程的有( )
①3(x+1)2=2(x+1);②
+
-2=0;③mx2=nx;④x2+2x=x2-1;⑤3x2=x;⑥x2=0.
①3(x+1)2=2(x+1);②
| 1 |
| x2 |
| 1 |
| x |
| A、2个 | B、3个 | C、4个 | D、5个 |
若反比例函数y=
(k≠0)的图象过点(2,1),则这个函数的图象一定过点( )
| k |
| x |
| A、(2,-1) |
| B、(1,-2) |
| C、(-2,1) |
| D、(-2,-1) |
 如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证:
如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证: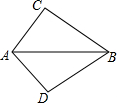 如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件
如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件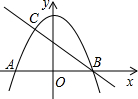 如图,抛物线y=-
如图,抛物线y=-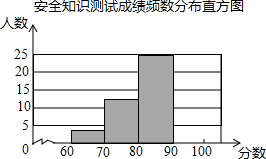 某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成).
某县为了了解初中生对安全知识掌握情况,抽取了50名初中生进行安全知识测试,并将测试成绩进行统计分析,绘制成了频数分布表和频数分布直方图(未完成). 如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E.
如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E.