题目内容
19．已知四个三角形的三个内角的比分别是1：3：4，2：5：7，1：3：5，2：6：9，在这四个三角形中，直角三角形有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据三角形的内角和是180°，按比例分配，可得最大角的度数，根据直角三角形的定义，可得答案．
解答 解：1：3：4的最大角是180°×$\frac{4}{1+3+4}$=90°，是直角三角形；
2：5：7的最大角是180°×$\frac{7}{2+5+7}$=90°，是直角三角形；
1：3：5的最大角是180°×$\frac{5}{1+3+5}$=100°，是钝角三角形；
2：6：9的最大角是180°×$\frac{9}{2+6+9}$≈94°，是钝角三角形．
故选：B．
点评 本题考查了三角形内角和定理，利用按比例分配计算出最大角是解题关键．
练习册系列答案
相关题目
如图，在△ABC中，AB＞AC，AD为∠BAC的平分线，AD的垂直平分线交BC的延长线于点F，交AB、AC于点E、G．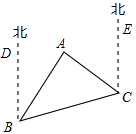
如图，A点在B点的北偏东40°方向，C点在B点的北偏东75°方向，A点在C点的北偏西50°方向，求从A点观测B，C两点的视角∠BAC的度数．
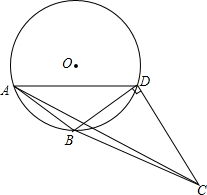如图，⊙O是△ABD的外接圆，在⊙O外取点C，使得∠BCD=∠BAD，且∠BDC=90°，若∠ADB=30°，求证：BC=2AB．
在正方形ABCD中，点E是边AD上任意一点，BE的垂直平分线交对角AC于点F，联结BE、BF，求∠EBF．