题目内容
10.在数轴上分别作出$\sqrt{13}$和-$\sqrt{7}$的对应点.分析 因为$\sqrt{13}=\sqrt{{2}^{2}+{3}^{2}}$,所以在数轴上以原点O向右数出2个单位(为点A)作为直角三角形的一条直角边,过点A作数轴的垂线并截取AB为3个单位长度,连接OB,求得OB,最后以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C即为表示$\sqrt{13}$的点;同理,根据$\sqrt{5}$=$\sqrt{{1}^{2}+{2}^{2}}$,$\sqrt{6}$=$\sqrt{{1}^{2}+{(\sqrt{5})}^{2}}$,$\sqrt{7}$=$\sqrt{{1}^{2}+{(\sqrt{6})}^{2}}$画出图形即可.
解答  解:如图所示,
解:如图所示,
点评 本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知四个三角形的三个内角的比分别是1:3:4,2:5:7,1:3:5,2:6:9,在这四个三角形中,直角三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.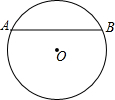 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )| A. | 24cm | B. | 13cm | C. | 14cm | D. | 15cm |
 按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.
按图那样堆放钢管,第一层(最上层)有5根,第二层有6根,第三层有7根,…那么,第n层有多少根?并求出第30层钢管的根数.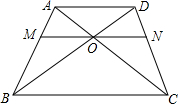 如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON.
如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON. 如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形.
如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形. 小明家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,一面墙的中间留出1米宽的进出门(门使用另外的材料).现备有足够砌15米长的围墙的材料,设猪圈与已有墙面垂直的墙的长度为x米.
小明家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,一面墙的中间留出1米宽的进出门(门使用另外的材料).现备有足够砌15米长的围墙的材料,设猪圈与已有墙面垂直的墙的长度为x米.