题目内容
11.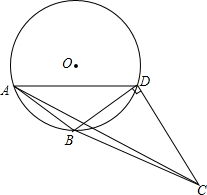 如图,⊙O是△ABD的外接圆,在⊙O外取点C,使得∠BCD=∠BAD,且∠BDC=90°,若∠ADB=30°,求证:BC=2AB.
如图,⊙O是△ABD的外接圆,在⊙O外取点C,使得∠BCD=∠BAD,且∠BDC=90°,若∠ADB=30°,求证:BC=2AB.
分析 作直径BE,连接DE、OA,根据圆周角定理证明△AOB是等边三角形,得到AB=$\frac{1}{2}$BE,证明△BDE≌△BDC,得到BC=BE,证明结论.
解答 证明: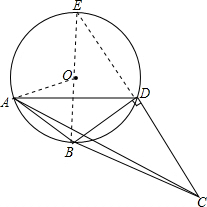 作直径BE,连接DE、OA,
作直径BE,连接DE、OA,
∠AOB=2∠ADB=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OB=$\frac{1}{2}$BE,
∵BE是⊙O的直径,
∴∠BDE=90°,
∵∠BED=∠BAD,∠BCD=∠BAD,
∴∠BCD=∠BED.
在△BDE和△BDC中,
$\left\{\begin{array}{l}{∠BED=∠BCD}\\{∠BDE=∠BDC}\\{BD=BD}\end{array}\right.$,
∴△BDE≌△BDC,
∴BC=BE,
∴BC=2AB.
点评 本题考查的是三角形的外接圆与外心的概念和性质、圆周角定理,正确作出辅助线、灵活运用圆周角定理和三角形全等的判定定理是解题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
19.已知四个三角形的三个内角的比分别是1:3:4,2:5:7,1:3:5,2:6:9,在这四个三角形中,直角三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.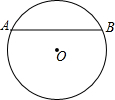 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )| A. | 24cm | B. | 13cm | C. | 14cm | D. | 15cm |
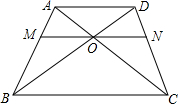 如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON.
如图,已知梯形ABCD中,AD∥BC,AC,BD交于O,过O作AD的平行线交AB于M,交CD于N.若AD=3cm,BC=5cm,求ON.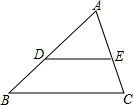 如图,在△ABC中,D、E分别在AB、AC上,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,如果AE=3.6cm,EC=2.4cm,AB=9cm.求AD和BD的长.
如图,在△ABC中,D、E分别在AB、AC上,且$\frac{AD}{AB}$=$\frac{AE}{AC}$,如果AE=3.6cm,EC=2.4cm,AB=9cm.求AD和BD的长. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值.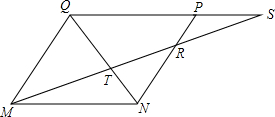 如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$.
如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$. 用直尺、圆规作图:如图,Rt△ABC中,∠C=90°,在AC上找一点D,使点D到AB,BC的距离相等.
用直尺、圆规作图:如图,Rt△ABC中,∠C=90°,在AC上找一点D,使点D到AB,BC的距离相等.