题目内容
8.抛物线y=$\frac{1}{2}$(x+$\frac{1}{3}$)2的开口方向向上,对称轴是x=-$\frac{1}{3}$,顶点坐标是(-$\frac{1}{3}$,0),与x轴的交点是(-$\frac{1}{3}$,0),当x=-$\frac{1}{3}$时,y有最小值为0; 当x$>-\frac{1}{3}$时,y随x的增大而增大.分析 根据二次函数的性质,得出开口方向,利用顶点式求出函数的最值与对称轴即可;令y=0得关于x的一元二次方程,求解得到两根,此即为与x轴的两交点坐标,进一步得出增减性.
解答 解:a=$\frac{1}{2}$,开口方向向上;
顶点为(-$\frac{1}{3}$,0),对称轴是x=-$\frac{1}{3}$;
令y=0,得x的两根为x1=x2=-$\frac{1}{3}$,
故与x轴的交点坐标(-$\frac{1}{3}$,0);
当x=-$\frac{1}{3}$时,y有最小值为0; 当x$>-\frac{1}{3}$时,y随x的增大而增大.
故答案为:向上,x=-$\frac{1}{3}$,(-$\frac{1}{3}$,0),(-$\frac{1}{3}$,0),-$\frac{1}{3}$,增大.
点评 此题考查了二次函数的性质,重点是注意函数的开口方向、对称轴及函数与坐标轴交点的问题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
19.已知四个三角形的三个内角的比分别是1:3:4,2:5:7,1:3:5,2:6:9,在这四个三角形中,直角三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.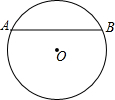 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
 如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )
如图,在⊙O中,弦AB的长为24cm,圆心O到AB的距离为5cm,则⊙O的半径长为( )| A. | 24cm | B. | 13cm | C. | 14cm | D. | 15cm |
 如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形.
如图,Rt△ABC中,∠ACB=90°,DE⊥AB交AC于F,则图中有6对相似三角形. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB、BC于D、E,求$\frac{DE}{BC}$的值.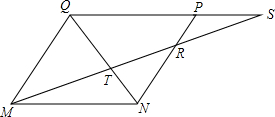 如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$.
如图,已知MNPQ为平行四边形,在QP的延长线上任取-点S,直线MS与NQ交于点T,与NP交于点R.求证:$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$. 如图,看图填空:
如图,看图填空: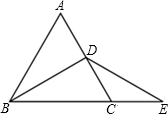 如图,在等边△ABC中,BD是高,延长BC到点E,使BC=2CE,求证:BD=DE.
如图,在等边△ABC中,BD是高,延长BC到点E,使BC=2CE,求证:BD=DE.