题目内容
1.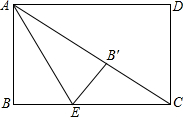 如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.
如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.
分析 先根据折叠得出BE=B′E,且∠AB′E=∠B=90°,可知△EB′C是直角三角形,由已知的BC=3BE得EC=2B′E,得出∠ACB=30°,从而得出AC与AB的关系,求出AB的长.
解答 解:由折叠得:BE=B′E,∠AB′E=∠B=90°,
∴∠EB′C=90°,
∵BC=3BE,
∴EC=2BE=2B′E,
∴∠ACB=30°,
在Rt△ABC中,AC=2AB,
∴AB=$\frac{1}{2}$AC=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了矩形的性质和翻折问题,明确翻折前后的图形全等是本题的关键,同时还运用了直角三角形中如果一条直角边是斜边的一半,那么这条直角边所对的锐角是30°这一结论,是常考题型.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
11.$\sqrt{64}$的算术平方根是( )
| A. | 8 | B. | ±8 | C. | $2\sqrt{2}$ | D. | ±$2\sqrt{2}$ |
12.说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 含30°的直角三角形 | D. | 顶角为45°的等腰三角形 |
9.已知a≠0,下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | (a2)3=a5 | C. | a2•a4=a8 | D. | a4÷a3=a |
16. 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠A=30°,BC=2$\sqrt{3}$,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )| A. | $\frac{15\sqrt{3}}{4}$-$\frac{3}{2}π$ | B. | $\frac{15\sqrt{3}}{2}$-$\frac{3}{2}π$ | C. | $\frac{7\sqrt{3}}{4}$-$\frac{π}{6}$ | D. | $\frac{7\sqrt{3}}{2}$-$\frac{π}{6}$ |
13.关于?ABCD的叙述,正确的是( )
| A. | 若AB⊥BC,则?ABCD是菱形 | B. | 若AC⊥BD,则?ABCD是正方形 | ||
| C. | 若AC=BD,则?ABCD是矩形 | D. | 若AB=AD,则?ABCD是正方形 |
11.-$\frac{3}{4}$的相反数是( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
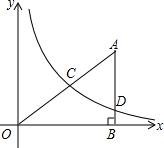 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 如图,点O是线段AB和线段CD的中点.
如图,点O是线段AB和线段CD的中点.