题目内容
6.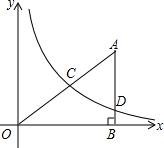 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y=$\frac{k}{x}$(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,(1)求反比例函数y=$\frac{k}{x}$的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
分析 (1)设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),由点A的坐标表示出点C的坐标,根据C、D点在反比例函数图象上结合反比例函数图象上点的坐标特征即可得出关于k、m的二元一次方程,解方程即可得出结论;
(2)由m的值,可找出点A的坐标,由此即可得出线段OB、AB的长度,通过解直角三角形即可得出结论;
(3)由m的值,可找出点C、D的坐标,设出过点C、D的一次函数的解析式为y=ax+b,由点C、D的坐标利用待定系数法即可得出结论.
解答 解:(1)设点D的坐标为(4,m)(m>0),则点A的坐标为(4,3+m),
∵点C为线段AO的中点,
∴点C的坐标为(2,$\frac{3+m}{2}$).
∵点C、点D均在反比例函数y=$\frac{k}{x}$的函数图象上,
∴$\left\{\begin{array}{l}{k=4m}\\{k=2×\frac{3+m}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=1}\\{k=4}\end{array}\right.$.
∴反比例函数的解析式为y=$\frac{4}{x}$.
(2)∵m=1,
∴点A的坐标为(4,4),
∴OB=4,AB=4.
在Rt△ABO中,OB=4,AB=4,∠ABO=90°,
∴OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=4$\sqrt{2}$,cos∠OAB=$\frac{AB}{OA}$=$\frac{4}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
(3))∵m=1,
∴点C的坐标为(2,2),点D的坐标为(4,1).
设经过点C、D的一次函数的解析式为y=ax+b,
则有$\left\{\begin{array}{l}{2=2a+b}\\{1=4a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=3}\end{array}\right.$.
∴经过C、D两点的一次函数解析式为y=-$\frac{1}{2}$x+3.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、解直角三角形以及待定系数法求函数解析式,解题的关键是:(1)由反比例函数图象上点的坐标特征找出关于k、m的二元一次方程组;(2)求出点A的坐标;(2)求出点C、D的坐标.本题属于基础题,难度不大,但考查的知识点较多,解决该题型题目时,利用反比例函数图象上点的坐标特征找出方程组,通过解方程组得出点的坐标,再利用待定系数法求出函数解析式即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. |  | B. |  | C. |  | D. |  |
| 成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
| 人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次测试成绩的众数是55分 | |
| C. | 该班学生这次测试成绩的中位数是60分 | |
| D. | 该班学生这次测试成绩的平均数是59分 |
| A. | (-5)0=0 | B. | x2+x3=x5 | C. | (ab2)3=a2b5 | D. | 2a2•a-1=2a |
| A. | 袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球 | |
| B. | 天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 | |
| C. | 某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖 | |
| D. | 连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
| A. | 2 | B. | -2 | C. | ±2 | D. | -$\root{3}{2}$ |
 已知二次函数y=x2-(2k+1)x+k2+k(k>0)
已知二次函数y=x2-(2k+1)x+k2+k(k>0)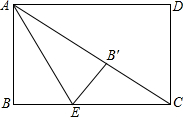 如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.
如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.