题目内容
10. 如图,点O是线段AB和线段CD的中点.
如图,点O是线段AB和线段CD的中点.(1)求证:△AOD≌△BOC;
(2)求证:AD∥BC.
分析 (1)由点O是线段AB和线段CD的中点可得出AO=BO,CO=DO,结合对顶角相等,即可利用全等三角形的判定定理(SAS)证出△AOD≌△BOC;
(2)结合全等三角形的性质可得出∠A=∠B,依据“内错角相等,两直线平行”即可证出结论.
解答 证明:(1)∵点O是线段AB和线段CD的中点,
∴AO=BO,CO=DO.
在△AOD和△BOC中,有$\left\{\begin{array}{l}{AO=BO}\\{∠AOD=∠BOC}\\{CO=DO}\end{array}\right.$,
∴△AOD≌△BOC(SAS).
(2)∵△AOD≌△BOC,
∴∠A=∠B,
∴AD∥BC.
点评 本题考查了全等三角形的判定与性质以及平行线的判定定理,解题的关键是:(1)利用SAS证出△AOD≌△BOC;(2)找出∠A=∠B.本题属于基础题,难度不大,解决该题型题目时,根据全等三角形的判定定理证出两三角形全等,结合全等三角形的性质找出相等的角,再依据平行线的判定定理证出两直线平行即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列运算中,正确的是( )
| A. | x3•x=x4 | B. | (-3x)2=6x2 | C. | 3x3-2x2=x | D. | x6÷x2=x3 |
5.一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
| A. | 13cm | B. | 14cm | C. | 13cm或14cm | D. | 以上都不对 |
15.下列说法正确的是( )
| A. | 袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球 | |
| B. | 天气预报“明天降水概率10%”,是指明天有10%的时间会下雨 | |
| C. | 某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖 | |
| D. | 连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 |
19.-$\frac{1}{6}$的相反数是( )
| A. | $\frac{1}{6}$ | B. | -6 | C. | 6 | D. | -$\frac{1}{6}$ |
20.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (-2a2)3÷($\frac{a}{2}$)2=-16a4 | ||
| C. | 3a-1=$\frac{1}{3a}$ | D. | (2$\sqrt{3}$a2-$\sqrt{3}$a)2÷3a2=4a2-4a+1 |
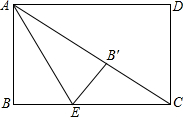 如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.
如图,矩形ABCD中,对角线AC=2$\sqrt{3}$,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB=$\sqrt{3}$.