题目内容
6.已知:反比例函数y=$\frac{p}{x}$上两点(x1,y1),(x2,y2),若x1>0>x2,则y1<0<y2.(1)判断p的符号为负(正、负);
(2)已知函数y=$\frac{4}{x}$与正比例函数y=kx交于(a,b),(c,d)两点,试探究3a2d-3abc+5的值.
分析 (1)根据当x1>0>x2,则y1<0<y2,即可判断出p的符号.
(2)根据题意得出a=-c,b=-d,代入即可求得3a2d-3abc+5的值.
解答 解:(1)∵反比例函数y=$\frac{p}{x}$上两点(x1,y1),(x2,y2),若x1>0>x2,则y1<0<y2,
∴反比例函数的图象在二四象限,
∴p<0,
故答案为负.
(2)由题意可知a=-c,b=-d,
∴3a2d-3abc+5
=3(-c)2d-3(-c)•(-d)•c+5
=3c2d-3c2d+5
=5.
点评 本题考查了反比例函数和一次函数的交点以及反比例函数的性质,(2)根据题意得出a=-c,b=-d是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.化简|a-2|+($\sqrt{2-a}$)2的结果是( )
| A. | 4-2a | B. | 0 | C. | 2a-4 | D. | 4 |
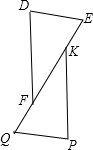 如图,△DEF≌△PQK,DE=5cm,EF=8cm,DF=7cm,QF=3cm.请求出图中其他线段的长度.
如图,△DEF≌△PQK,DE=5cm,EF=8cm,DF=7cm,QF=3cm.请求出图中其他线段的长度.
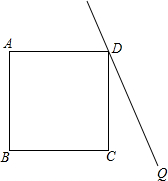 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.