题目内容
11.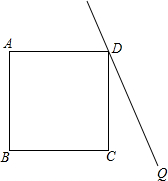 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.(1)依题意补全图形;
(2)若∠QDC=25°,求∠DPA的度数;
(3)探究线段AE、EF、FP的等量关系并加以证明.
分析 (1)根据题意直接画出图形得出即可;
(2)利用对称的性质以及等角对等边进而得出答案;
(3)由轴对称的性质可得:EC=EA,FC=FP,∠DPA=∠DAP=∠DCF,进而利用勾股定理得出答案.
解答 解:(1)如图1所示: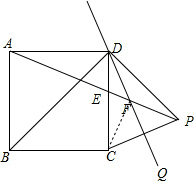
(2)∵∠QDP=∠QDC=25°,DP=DC=AD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠QDP=∠QDC=25°,
∴∠PDA=140°,
∴∠DPA=$\frac{180°-140°}{2}$=20°;
(3)AE2=EF2+FP2,
∵△DAE≌△DCE,△DFP≌△DFC,
可得:EC=EA,FC=FP,
∠DPA=∠DAP=∠DCF,
∵∠DEA+∠DAP=∠CEF+∠DCF=90°,
∴∠EFC=∠ADC=90°,
∴AE2=EF2+FP2
点评 此题主要考查了正方形的性质以及勾股定理和等腰三角形的性质等知识,利用轴对称的性质得出对应边相等是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.用同样大小的黑色的小三角形按如图所示的规律摆放,则第100个图形有( )个黑色的小三角形.


| A. | 300 | B. | 303 | C. | 306 | D. | 309 |
20.随机抛掷一枚质地均匀的硬币两枚,两次都是正面朝上的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
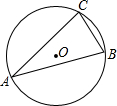 如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.
如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.