题目内容
8.若1×22-2×32=-1×2×7;(1×22-2×32)+(3×42-4×52)=-2×3×11;
(1×22-2×32)+(3×42-4×52)+(5×62-6×72)=-3×4×15;
则(1×22-2×32)+(3×42-4×52)+…+[(2n-1)(2n)2-2n(2n+1)2]=-n(n+1)(4n+3).
分析 仔细观察题目提供的三个算式,发现结果和式子序列号之间的关系,然后将这个规律表示出来即可.
解答 解:∵1×22-2×32=-1×2×7=-1×2×(4×1+3);
(1×22-2×32)+(3×42-4×52)=-2×3×11=-2×3×(4×2+3);
(1×22-2×32)+(3×42-4×52)+(5×62-6×72)=-3×4×15═-3×4×(4×3+3);
…
(1×22-2×32)+(3×42-4×52)+…+[(2n-1)(2n)2-2n(2n+1)2]=-n(n+1)(4n+3),
故答案为:-n(n+1)(4n+3).
点评 本题考查了数字的变化类问题,仔细观察提供的算式,用含有n的代数式表示出来即可.

练习册系列答案
相关题目
18.将6个边长是1的正方形无缝隙铺成一个矩形,则这个矩形的对角线长等于( )
| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
19.图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示.
(1)根据图2填表:
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.

(1)根据图2填表:
| x(min) | 0 | 3 | 6 | 8 | 12 | … |
| y(m) | 5 | 70 | 5 | 54 | 5 | … |
(3)根据图中的信息,请写出摩天轮的直径.

18.描述一组数据离散程度的统计量是( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
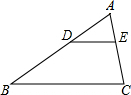 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}=\frac{1}{3}$,DE=6,则BC的长是18.
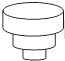
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}=\frac{1}{3}$,DE=6,则BC的长是18.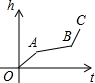 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )


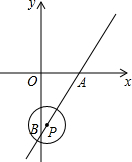 已知如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
已知如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.


