题目内容
1.已知关于x的方程kx2-x-$\frac{2}{k}$=0(k≠0).(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个根都为整数,求整数k的值,并求出方程的根.
分析 (1)先判断方程为关于x的一元二次方程,再计算出△=9,于是根据判别式的意义可判断方程总有两个不相等的实数根;
(2)利用求根公式解方程得到x1=$\frac{2}{k}$,x2=-$\frac{1}{k}$,然后利用整数的整除性确定k的值.
解答 解:(1)由题知:△=(-1)2-4×k×(-$\frac{2}{k}$)
=1+8
=9>0.
∴方程总有两个不相等的实数根.
(2)解:由求根公式得:x=$\frac{1±\sqrt{9}}{2k}$,
∴x1=$\frac{2}{k}$,x2=$\frac{-1}{k}$,
又∵方程的两个根都为整数,且k也为整数,
∴k的值为1或-1,
当k=1时,两根为x1=2,x2=-1;
当k=-1时,两根为x1=-2,x2=1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
6.下列运算正确的是( )
| A. | a3•a2=a6 | B. | 3-1=-3 | C. | (-2a)3=-8a3 | D. | 20160=0 |
13.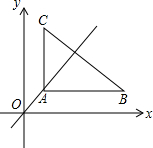 如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
 如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )
如图,等腰三角形ABC位于第一象限,∠CAB=90°,腰长为4,顶点A在直线y=x上,点A的横坐标为1,等腰三角形ABC的两腰分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$于等腰三角形ABC有公共点,则k的最大值为( )| A. | 5 | B. | $\frac{25}{4}$ | C. | 9 | D. | 16 |
16.将四个编号为1,2,3,4的小球随机放入4个编号为1,2,3,4的盒子中.记f(i)为第i个盒子中小球的编号与盒子编号的差的绝对值.则f(1)+f(2)+f(3)+f(4)=4的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{5}{24}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{24}$ |
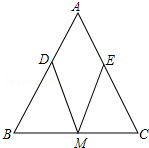 如图,在△ABC中,M是BC的中点,D、E分别是AB、AC边上的点,BD=CE,且MD=ME,求证:AB=AC.
如图,在△ABC中,M是BC的中点,D、E分别是AB、AC边上的点,BD=CE,且MD=ME,求证:AB=AC. 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).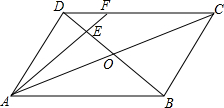 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,若DF=2,则FC=4.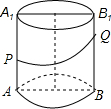 如图所示,已知圆柱的高为80cm.底面半径为10cm,轴截面上有两点P,Q.PA=40cm.B1Q=30cm.则圆柱的侧面上P,Q两点的最短距离是多少?
如图所示,已知圆柱的高为80cm.底面半径为10cm,轴截面上有两点P,Q.PA=40cm.B1Q=30cm.则圆柱的侧面上P,Q两点的最短距离是多少?