题目内容
10.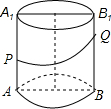 如图所示,已知圆柱的高为80cm.底面半径为10cm,轴截面上有两点P,Q.PA=40cm.B1Q=30cm.则圆柱的侧面上P,Q两点的最短距离是多少?
如图所示,已知圆柱的高为80cm.底面半径为10cm,轴截面上有两点P,Q.PA=40cm.B1Q=30cm.则圆柱的侧面上P,Q两点的最短距离是多少?
分析 利用圆柱的侧面展开图,作PE⊥BB1于E,在RT△PQE中利用勾股定理解决问题.
解答 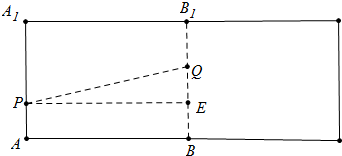 解:如图是圆柱的侧面展开图,PQ的长就是圆柱的侧面上P,Q两点的最短距离,作PE⊥BB1于E,
解:如图是圆柱的侧面展开图,PQ的长就是圆柱的侧面上P,Q两点的最短距离,作PE⊥BB1于E,
在RT△PEQ中,∵PE=10π,QE=80-30-40=10,
∴PQ=$\sqrt{P{E}^{2}+Q{E}^{2}}$=$\sqrt{100{π}^{2}+100}$=10•$\sqrt{{π}^{2}+1}$.
∴圆柱的侧面上P,Q两点的最短距离是10•$\sqrt{{π}^{2}+1}$cm.
点评 本题考查最短问题、两点之间线段最短,解题的关键是把立体图形转化为平面图形,利用勾股定理解决,属于中考常考题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
18.已知∠1=42°45′,则∠1的余角等于( )
| A. | 47°55′ | B. | 47°15′ | C. | 48°15′ | D. | 137°55′ |
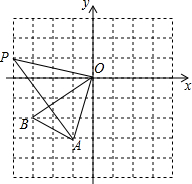 如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.
如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.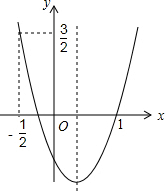 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.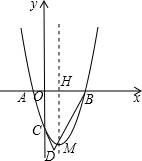 如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.
如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.