题目内容
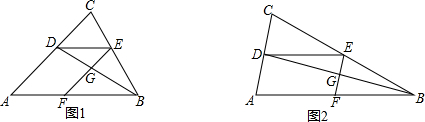
4. 如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )
如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{12}$ |
分析 设DF=a,则DF=AE=a,AF=EB=2a,由△HFD∽△BFA,得$\frac{HD}{AB}$=$\frac{DF}{AF}$=$\frac{HF}{FB}$=$\frac{1}{2}$,求出FH,再由HD∥EB,得△DGH∽△EGB,得$\frac{HG}{GB}$=$\frac{HD}{EB}$=$\frac{1.5a}{2a}$=$\frac{3}{4}$,求出BG即可解决问题.
解答  解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AF=2DF,设DF=a,则DF=AE=a,AF=EB=2a,
∵HD∥AB,
∴△HFD∽△BFA,
∴$\frac{HD}{AB}$=$\frac{DF}{AF}$=$\frac{HF}{FB}$=$\frac{1}{2}$,
∴HD=1.5a,$\frac{FH}{BH}$=$\frac{1}{3}$,
∴FH=$\frac{1}{3}$BH,
∵HD∥EB,
∴△DGH∽△EGB,
∴$\frac{HG}{GB}$=$\frac{HD}{EB}$=$\frac{1.5a}{2a}$=$\frac{3}{4}$,
∴$\frac{BG}{HB}$=$\frac{4}{7}$,
∴BG=$\frac{4}{7}$HB,
∴$\frac{HF}{BG}$=$\frac{\frac{1}{3}BH}{\frac{4}{7}BH}$=$\frac{7}{12}$.
故选B.
点评 本题考查相似三角形的性质和判定、菱形的性质、比例的选择等知识,解题的关键是利用相似三角形的性质解决问题,学会设参数,属于中考常考题型.

练习册系列答案
相关题目
12. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | ac>bc | B. | -a-c>-b-c | C. | -a<-b<-c | D. | |a-b|=a-b |
 如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π. 如图,OA表示南偏西20°方向的一条射线,∠AOB=90°,那么OB的方向可表示为南偏东70°.
如图,OA表示南偏西20°方向的一条射线,∠AOB=90°,那么OB的方向可表示为南偏东70°.