题目内容
16.在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD.如果AD=4,BC=10,那么梯形ABCD的面积等于49.分析 首过D作DE∥AC交BC的延长线于E,过D作DF⊥BC于F,先求出△BDEE是等腰直角三角形推出DFF与BE的关系,进而根据梯形的面积公式即可求解.
解答 解:过D作DE∥AC交BC的延长线于E,过D作DF⊥BC于F.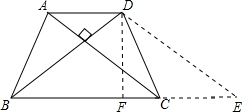
∵AD∥CB,DE∥AC,
∴四边形ADEC是平行四边形,
∴DE=AC,AD=CE=4
∵等腰梯形ABCD中,AB=CD,
∴DE=AC=BD,
∵AC⊥BD,CE∥AD,
∴DE⊥BD,
∴△BDE是等腰直角三角形,
又∵AD=4,BC=10,
∴DF=$\frac{1}{2}$BE=$\frac{1}{2}$(AD+BC)=$\frac{1}{2}$(4+10)=7,
∴梯形的面积为:$\frac{1}{2}$(4+10)×7=49.
故答案为:49.
点评 本题考查等腰梯形的性质,难度不大,注意在解题的过程中运算平行线的性质,另外要掌握等腰梯形的面积还等于对角线互相两条对角线乘积的一半.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
4. 如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )
如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )
 如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )
如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若$\frac{AF}{DF}$=2,则$\frac{HF}{BG}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{7}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{12}$ |
10.已知一次函数y=(m-1)x+5-2m,若m的取值范围是1<m<$\frac{5}{2}$,则这个函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
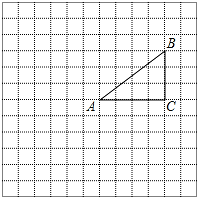 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′. 如图,反比例函数$y=-\frac{2}{x}$的图象与直线$y=-\frac{1}{2}x$的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为4.
如图,反比例函数$y=-\frac{2}{x}$的图象与直线$y=-\frac{1}{2}x$的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为4.