题目内容
19．
如图，在半⊙O中，P为直径AB上的一个动点，点C，D为半圆的三等分点，若AB=12，则图中阴影部分的面积为6π．
分析 连接OC、OD，利用同底等高的三角形面积相等可知阴影部分的面积等于扇形OCD的面积，然后计算扇形面积就可．
解答 解：连接OC、OD、CD．
∵△COD和△CPD等底等高，
∴S△COD=S△PCD．
∵点C，D为半圆的三等分点，
∴∠COD=180°÷3=60°，
∴阴影部分的面积=S扇形COD=$\frac{60π×{6}^{2}}{360}$=6π．
故答案为：6π．
点评 此题主要考查了扇形面积求法，利用已知得出理解阴影部分的面积等于扇形OCD的面积是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知一次函数y=ax+b和y=kx的图象相交于点P，则根据图中信息可得二元一次方程组$\left\{\begin{array}{l}{y=ax+b}\\{kx-y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．
4．
如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若$\frac{AF}{DF}$=2，则$\frac{HF}{BG}$的值为（ ）
如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若$\frac{AF}{DF}$=2，则$\frac{HF}{BG}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{7}{12}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{12}$ |
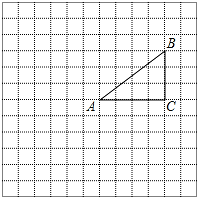如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．
直角三角形的一个角是60°，用四个这样的直角三角形拼成如图所示的正方形ABCD，若正方形EFGH的边长是$\sqrt{3}$-1，则正方形ABCD的边长是2．