题目内容
8.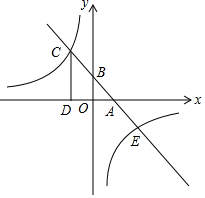 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.(1)△ADC 的面积;
(2)求反比例函数y=$\frac{{k}_{2}}{x}$与一次函数的y=k1x+b表达式.
分析 (1)求出AD=CD,解直角三角形求出AD、CD,根据三角形的面积公式求出即可;
(2)把C的坐标代入反比例函数的解析式,即可求出k2,把B、C的坐标代入一次函数的解析式,即可求出b和k1.
解答 解:(1)∵OA=OB,
∠ABO=∠OAB=45°,
∵CD⊥x轴于D,
∴∠ADC=90°,
∴∠BAD=∠ACD=45°,
∴CD=AD,
∵AC=2$\sqrt{2}$,
∴CD=AD=$\frac{\sqrt{2}}{2}$AC=2,
∴△ADC 的面积为$\frac{1}{2}×AD×CD$=$\frac{1}{2}×2×2$=2;
(2)∵OA=1,AD=2,
∴OD=1,
∵CD=2,
∴C的坐标为(-1,2),
∵点C在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,
∴2=$\frac{{k}_{2}}{-1}$,
∴k2=-2,
∴反比例函数的表达式为y=-$\frac{2}{x}$;
∵一次函数y=k1x+b过B(0,1),C(-1,2),
∴代入得:$\left\{\begin{array}{l}{b=1}\\{-{k}_{1}+b=2}\end{array}\right.$,
解得:b=1,k1=-1,
∴一次函数的表达式为y=-x+1.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式等知识点,能正确用待定系数法求出函数的解析式是解此题的关键,注意数形结合思想的运用.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
3.一家面临倒闭的企业在“调整产业结构,转变经营机制”的改革后,扭亏为盈.下表是该企业2015年8~12月、2016年第一季度的月利润统计表:
根据以上信息,解答下列问题:
(1)2015年8月至2016年1月该企业利润的月平均利润为45万元,月利润的中位数为45万元;
(2)已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
| 时间 | 2015年 | 2016年 | ||||||
| 8月 | 9月 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 | |
| 利润(万元) | 48 | 46 | 42 | 44 | 40 | 50 | 72 | |
(1)2015年8月至2016年1月该企业利润的月平均利润为45万元,月利润的中位数为45万元;
(2)已知该企业2016年2、3月份的月利润的平均增长率相同,求这个平均增长率和2月份的月利润.
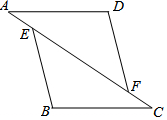 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:DF=BE.
如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:DF=BE. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.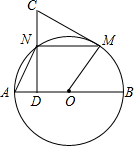 如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C.
如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C. 如图,二次函数y=(x+m)2+k的图象与x轴交于A、B两点,顶点M的坐标为(1,-4).
如图,二次函数y=(x+m)2+k的图象与x轴交于A、B两点,顶点M的坐标为(1,-4).