题目内容
20.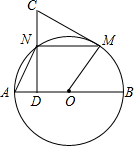 如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C.
如图,AB为圆O的直径,点M为圆上不与A,B重合的动点,点N平分弧AM,ND⊥AB于点D,过点M的切线交DN的延长线于点C.(1)若MC∥AB,试判断AD与CN的数量关系,判断四边形OMCD的形状,并都给出理由;
(2)填空:当∠ANM=120°时,四边形ANMO是菱形.
分析 (1)根据CM是⊙O的切线,得到OM⊥CM,根据已知条件得到∠C=∠M=∠CDO=90°,于是得到四边形OMCD是矩形,连接ON,根据全等三角形的性质得到∠A=∠OMN,根据余角的性质得到∠AND=∠CMN,根据全等三角形的判定和性质得到AD=CN;
(2)如图2,连接ON,根据全等三角形的性质得到∠ANO=∠MNO=$\frac{1}{2}∠$ANM=60°,推出△AON与△MON是等边三角形,于是得到AN=AO=MN=OM,即可得到结论.
解答 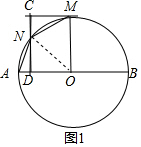 解:(1)AD=CN,四边形OMCD是矩形,
解:(1)AD=CN,四边形OMCD是矩形,
理由:∵CM是⊙O的切线,
∴OM⊥CM,
∵ND⊥AB,
∴CD⊥AB,
∴∠C=∠M=∠CDO=90°,
∴四边形OMCD是矩形,
连接ON,
∵点N平分弧AM,
∴$\widehat{AN}$=$\widehat{MN}$,
∴AN=MN,
在△AON与△NOM中,$\left\{\begin{array}{l}{AO=OM}\\{AN=MN}\\{ON=ON}\end{array}\right.$,
∴△AON≌△NOM,
∴∠A=∠OMN,
∵∠A+∠AND=∠OMN+∠CMN=90°,
∴∠AND=∠CMN,
在△AND与△NCM中,$\left\{\begin{array}{l}{∠ADN=∠CNM=90°}\\{∠AND=∠CMN}\\{AN=MN}\end{array}\right.$,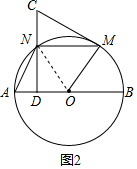
∴△AND≌△NCM,
∴AD=CN;
(2)当∠ANM=120°时,四边形ANMO是菱形;
如图2,连接ON,
∵点N平分弧AM,
∴$\widehat{AN}$=$\widehat{MN}$,
∴AN=MN,
在△AON与△NOM中,$\left\{\begin{array}{l}{AO=OM}\\{AN=MN}\\{ON=ON}\end{array}\right.$,
∴△AON≌△NOM,
∴∠ANO=∠MNO=$\frac{1}{2}∠$ANM=60°,
∴△AON与△MON是等边三角形,
∴AN=AO=MN=OM,
∴四边形ANMO是菱形.
故答案为:120.
点评 本题考查了切线的性质,菱形的判定,全等三角形的判定和性质,圆周角定理,矩形的判定,正确的作出辅助线是解题的关键.

| A. | 42.9×108 | B. | 4.29×108 | C. | 4.29×109 | D. | 4.3×109 |
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )| A. | 点B到直线l1的距离等于4 | B. | 点C到直线l1的距离等于5 | ||
| C. | 点C到AB的距离等于4 | D. | 点B到直线AC的距离等于5 |
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{{6}^{2}}$=±6 | D. | $\sqrt{(-5)^{2}}$=±5 |
 如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC.
如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且$\widehat{\widehat{BC}}$=$\widehat{CD}$,弦AD的延长线交切线PC于点E,连接AC. 如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.
如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.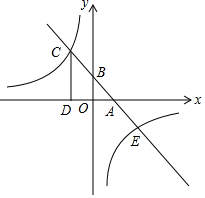 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.