题目内容
19．
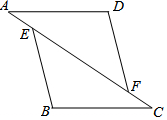如图，在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：DF=BE．
分析 根据两直线平行，内错角相等可得∠A=∠C，再求出AE=CF，然后利用“角角边”证明△ADF和△CBE全等，根据全等三角形对应边相等证明即可．
解答 证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
即AF=CE，
∵在△ADF和△CBE中，$\left\{\begin{array}{l}{∠B=∠D}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$，
∴△ADF≌△CBE（AAS），
∴DF=BE．
点评 本题考查了全等三角形的判定与性质，平行线的性质，熟练掌握三角形全等的判定方法并求出三角形全等的条件是解题的关键．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
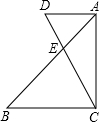将一副三角板按如图所示的方式摆放，其中∠CAD=∠ACB=90°，∠ACD=30°，∠B=45°，则有下列结论：①AD：BC=AE：CE；②∠BEC=70°；③BC=$\sqrt{3}$AD；④CD：AB=2：$\sqrt{6}$，其中正确结论的序号是③④．（把所有正确结论的序号都填在横线上）
如图，以AB为直径的⊙O经过点C，过点C作⊙O的切线交AB的延长线于点P，D是⊙O上于点，且$\widehat{\widehat{BC}}$=$\widehat{CD}$，弦AD的延长线交切线PC于点E，连接AC．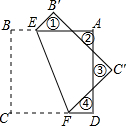
如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为32．
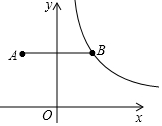在平面直角坐标系中，点A（-2，3）关于y轴的对称点为点B，连接AB，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点B，过点B作BC⊥x轴于点C，点P是该反比例函数图象上任意一点．
如图，在△ABC和△AEF中，AC∥EF，AB=FE，AC=AF，求证：∠B=∠E．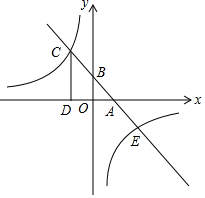
如图，已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A，B 两点，且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C，E 两点，点 C 在第二象限，过点 C 作CD⊥x轴于点 D，AC=2$\sqrt{2}$，OA=OB=1．