题目内容
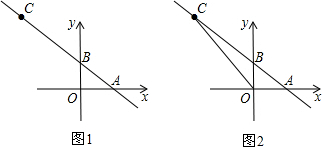
10. 如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..
如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..
分析 先求出BC=6,AB=3$\sqrt{2}$+$\sqrt{6}$.以BC所在直线为x轴,y轴经过点A,建立坐标系,则A(0,3+$\sqrt{3}$),设P(a,0),则Q(a+3,0),D($\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$),求出AP+DQ,利用几何意义,结合对称性,即可得出结论.
解答 解:由题意,∠A=60°.
由正弦定理可得$\frac{2\sqrt{6}}{\frac{\sqrt{2}}{2}}=\frac{BC}{\frac{\sqrt{3}}{2}}=\frac{AB}{\frac{\sqrt{6}+\sqrt{2}}{4}}$,
∴BC=6,AB=3$\sqrt{2}$+$\sqrt{6}$.
以BC所在直线为x轴,y轴经过点A,建立坐标系,则A(0,3+$\sqrt{3}$),
设P(a,0),则Q(a+3,0),D($\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$)
∴AP+DQ=$\sqrt{(a-0)^{2}+[0-(3+\sqrt{3})^{2}}$+$\sqrt{(a-\frac{3+\sqrt{3}}{2})^{2}+(0-\frac{3+\sqrt{3}}{2})^{2}}$,
表示x轴上的点(a,0)与A(0,3+$\sqrt{3}$),($\frac{3+\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$)的距离和,
利用对称性,($\frac{3+\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$)关于x轴的对称点的坐标为E($\frac{3+\sqrt{3}}{2}$,-$\frac{3+\sqrt{3}}{2}$),
可得AP+DQ的最小值为AE=$\sqrt{(0-\frac{3+\sqrt{3}}{2})^{2}+(3+\sqrt{3}+\frac{3+\sqrt{3}}{2})^{2}}$=$\frac{3\sqrt{10}+\sqrt{30}}{2}$.
故答案为:$\frac{3\sqrt{10}+\sqrt{30}}{2}$.
点评 本题考查解三角形的运用,考查距离公式的运用,考查学生分析解决问题的能力,难度大.

 考前必练系列答案
考前必练系列答案 如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )
如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )| A. | $\frac{1}{2}$cm2 | B. | 1cm2 | C. | 2cm2 | D. | 4cm2 |
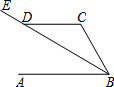 如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )| A. | 150° | B. | 130° | C. | 120° | D. | 100° |
| A. | -5 | B. | 0 | C. | π | D. | $\sqrt{2}$ |