题目内容
15．若实数a、b满足|a+2|+$\sqrt{b-4}$=0，则a2+b2的平方根是±2$\sqrt{5}$．分析 根据非负数的性质列式求出a和b的值，然后代入求出a2+b2的值，再根据平方根的定义解答．
解答 解：由题意得，a+2=0，b-4=0，
解得a=-2，b=4，
所以a2+b2=4+16=20，
∴a2+b2的平方根±2$\sqrt{5}$．
故答案为：±2$\sqrt{5}$．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
阅读快车系列答案
相关题目
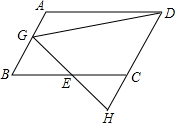如图，在?ABCD中，E为BC中点，过点E作EG⊥AB于G，连结DG，延长DC，交GE的延长线于点H．已知BC=10，∠GDH=45°，DG=8$\sqrt{2}$．求CD的长．
如图，在△ABC中，∠B=45°，∠C=75°，AC=2$\sqrt{6}$，AC的中点为D，若长度为3的线段PQ（P在Q的左侧）在直线BC上滑动，则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$．．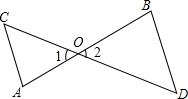
如图，AB和CD相交于点O，∠C=∠1，∠D=∠2，求证：∠A=∠B．
已知关于x的一元二次方程mx2+（3m+1）x+3=0．