题目内容
2.已知,直线AB分别交x、y轴于A(4,0)、B两点,C(-4,a)为直线y=-x与AB的公共点.(1)求点B的坐标;
(2)已知动点M在直线y=x+6上,是否存在点M使得S△OMB=S△OMA?若存在,求出点M的坐标;若不存在,说明理由.
(3)已知点E(0,8),P是x轴正半轴上的动点,Q是y轴正半轴上的动点,Q在点E上方,OP=EQ,QH是∠OQP的角平分线交直线CO于H.求OE,PQ,OH之间的数量关系.
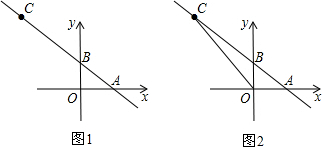
分析 (1)由点C在直线y=-x上可得出a的值,从而得出C点的坐标,设直线AB的解析式为y=kx+b,代入A、C点的坐标,由待定系数法即可求出直线AB的解析式,令x=0即可求出点B的坐标;
(2)假设存在,设点M的坐标为(m,m+6).由O、A、B、M点的坐标结合三角形的面积公式即可找出关于m的一元一次方程,解方程即可求出m的值,代入M点的坐标中即可得出结论;
(3)设点H(t,-t),P(a,0),QH与x轴的交点为M,理由勾股定理即可得出PQ2=2a(a+8)+64,由QH是∠OQP的角平分线,利用角平分线的性质即可得出$\frac{OM}{a+8}$=$\frac{a-OM}{PQ}$=$\frac{a}{a+8+PQ}$,结合$\frac{OM}{t}$=$\frac{OQ}{OQ+t}$,即可得出a(a+8)=t(PQ+8),即$\frac{P{Q}^{2}-64}{2}$=$\frac{OH(8+PQ)}{\sqrt{2}}$,整理后即是PQ=$\sqrt{2}$OH+8=$\sqrt{2}$OH+OE.
解答 解:(1)∵点C(-4,a)为直线y=-x上一点,
∴a=-1×(-4)=4,
∴点C(-4,4).
设直线AB的解析式为y=kx+b,
将A、C坐标分别代入直线AB的解析式得:$\left\{\begin{array}{l}{0=4k+b}\\{4=-4k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{1}{2}$x+2,
令x=0时,y=2,
∴点B的坐标为(0,2).
(2)假设存在,设点M的坐标为(m,m+6).
∵点A(4,0)、点B(0,2)、点M(m,m+6),
∴OA=4,OB=2,|Mx|=|m|,|My|=|m+6|,
∴S△OMA=$\frac{1}{2}$OA•|My|=2|m+6|;
S△OMB=$\frac{1}{2}$OB•|Mx|=|m|.
∵S△OMB=S△OMA,
∴2|m+6|=|m|,
∴2(m+6)=m或2(m+6)=-m,
解得:m1=-12,m2=-4.
∵-12+6=-6,-4+6=2,
∴M点的坐标为(-12,-6)或(-4,2).
故动点M在直线y=x+6上,存在点M使得S△OMB=S△OMA,点M的坐标为(-12,-6)或(-4,2).
(3)设点H(t,-t),P(a,0),QH与x轴的交点为M,如图所示,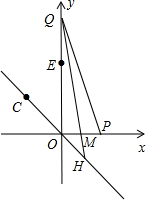
∴OH=$\sqrt{2}$t,PQ2=(a+8)2+a2=2a(a+8)+64.
∵QH是∠OQP的角平分线,
∴$\frac{OM}{MP}$=$\frac{OQ}{PQ}$,即$\frac{OM}{a-OM}$=$\frac{a+8}{PQ}$,
∴$\frac{OM}{a+8}$=$\frac{a-OM}{PQ}$=$\frac{a}{a+8+PQ}$.
∵$\frac{OM}{t}$=$\frac{OQ}{OQ+t}$,即$\frac{OM}{a+8}$=$\frac{t}{a+8+t}$,
∴$\frac{a}{a+8+PQ}$=$\frac{t}{a+8+t}$,$\frac{a}{8+PQ}$=$\frac{t}{a+8}$,
∴a(a+8)=t(PQ+8),即$\frac{P{Q}^{2}-64}{2}$=$\frac{OH(8+PQ)}{\sqrt{2}}$,
∴PQ-8=$\sqrt{2}$OH,
∴PQ=$\sqrt{2}$OH+8=$\sqrt{2}$OH+OE.
点评 本题考查了待定系数法求函数解析式、三角形的面积公式、角平分线的性质以及勾股定理,解题的关键是:(1)待定系数法求函数解析式;(2)根据三角形的面积相等得出关于m的一元一次方程;(3)通过角平分线的性质以及勾股定理得出等式,整理变形即可得出结论.本题属于中档题,(1)(2)没有难度;(3)难度不大,但用到知识点较多,而且分式的变形较繁琐,属于易丢分部分.

 如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..
如图,在△ABC中,∠B=45°,∠C=75°,AC=2$\sqrt{6}$,AC的中点为D,若长度为3的线段PQ(P在Q的左侧)在直线BC上滑动,则AP+DQ的最小值为$\frac{3\sqrt{10}+\sqrt{30}}{2}$..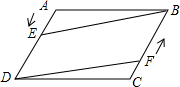 如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.
如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.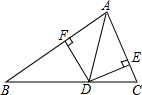 如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.
如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.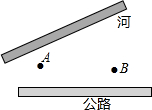 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.