题目内容
16.某商场代销甲、乙两种商品,其中甲种商品进价为120元/件,售价为130元/件,乙种商品进价为100元/件,售价为150元/件.(1)若商场用36000元购进这两种商品若干,销售完后可获利润6000元,则该商场购进甲、乙两种商品各多少件?(列方程组解答)
(2)若商场购进这两种商品共100件,设购进甲种商品x件,两种商品销售后可获总利润为y元,请写出y与x的函数关系式(不要求写出自变量x的范围),并指出购进甲种商品件数x逐渐增加时,总利润y是增加还是减少?
分析 (1)设购进甲商品x件,乙商品y件,根据进价36000元及利润6000元即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据总利润=甲种商品利润+乙种商品利润即可得出y关于x的一次函数关系式,根据一次函数的性质即可得出结论.
解答 解:(1)设购进甲商品x件,乙商品y件,
依题意得:$\left\{\begin{array}{l}{120x+100y=36000}\\{(130-120)x+(150-100)y=6000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=240}\\{y=72}\end{array}\right.$.
答:该商场购进甲商品240件,乙商品72件.
(2)依题意得:y=(130-120)x+(150-100)(100-x)=-40x+5000.
∵-40<0,
∴购进甲种商品件数x逐渐增加时,利润y逐渐减少.
点评 本题考查了一次函数的应用、解二元一次方程组以及一次函数的性质,根据数量关系列出二元一次方程组(或一次函数关系式)是解题的关键.

练习册系列答案
相关题目
5.某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
| 乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.

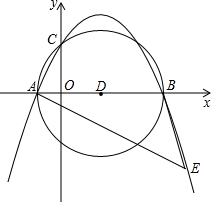 如图,在平面直角坐标系内,点O为坐标原点,抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C.
如图,在平面直角坐标系内,点O为坐标原点,抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C.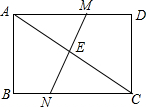 如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N.
如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N.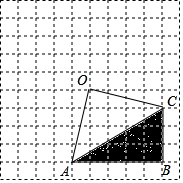 如图,在网格中有一个四边形图案.
如图,在网格中有一个四边形图案.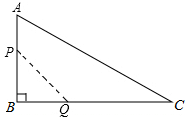 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)