题目内容
6.已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.
(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和$\frac{DE}{OD}$的值.
分析 (1)如图1中,连接OA.欲证明∠B=∠C,只要证明△AOC≌△AOB即可.
(2)由OH⊥AC,推出AH=CH,由H、O、B在一条直线上,推出BH垂直平分AC,推出AB=BC,由AB=AC,推出AB=AC=BC,推出△ABC为等边三角形,即可解决问题.
(3)过点B作BM⊥CE延长线于M,过E、O作EN⊥BC于N,OK⊥BC于K.设ME=x,则BE=2x,BM=$\sqrt{3}$x,在△BCM中,根据BC2=BM2+CM2,可得BM=5$\sqrt{3}$,推出sin∠BCM=$\frac{BM}{BC}$=$\frac{5\sqrt{3}}{14}$,推出NE=$\frac{15\sqrt{3}}{7}$,OK=$\frac{\sqrt{3}}{3}$CK=$\frac{7\sqrt{3}}{3}$,由NE∥OK,推出DE:OD=NE:OK即可解决问题.
解答 证明:(1)如图1中,连接OA.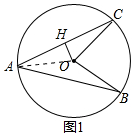
∵AB=AC,
∴$\widehat{AC}$=$\widehat{AB}$,
∴∠AOC=∠AOB,
在△AOC和△AOB中,
$\left\{\begin{array}{l}{OA=OA}\\{∠AOC=∠AOB}\\{OC=OB}\end{array}\right.$,
∴△AOC≌△AOB,
∴∠B=∠C.
解:(2)连接BC,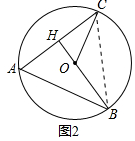
∵OH⊥AC,
∴AH=CH,
∵H、O、B在一条直线上,
∴BH垂直平分AC,
∴AB=BC,∵AB=AC,
∴AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°.
解:(3)过点B作BM⊥CE延长线于M,过E、O作EN⊥BC于N,OK⊥BC于K.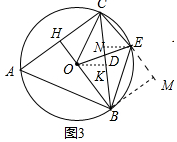
∵CH=7,
∴BC=AC=14,
设ME=x,
∵∠CEB=120°,
∴∠BEM=60°,
∴BE=2x,
∴BM=$\sqrt{3}$x,
△BCM中,∵BC2=BM2+CM2,
∴142=($\sqrt{3}$x)2+(6+x)2,
∴x=5或-8(舍弃),
∴BM=5$\sqrt{3}$,
∴sin∠BCM=$\frac{BM}{BC}$=$\frac{5\sqrt{3}}{14}$,
∴NE=$\frac{15\sqrt{3}}{7}$,
∴OK=$\frac{\sqrt{3}}{3}$CK=$\frac{7\sqrt{3}}{3}$,
∵NE∥OK,
∴DE:OD=NE:OK=45:49.
点评 本题考查圆综合题、全等三角形的判定和性质.线段的垂直平分线的性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,属于中考压轴题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 16.5 | B. | 16 | C. | 15 | D. | 14 |
| A. | 3 | B. | 4 | C. | 2 | D. | 1 |
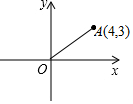 如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个.
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个. 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )