Question

11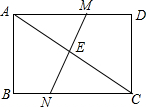．如图，在矩形ABCD中，AC是对角线，E是AC的中点，过E作MN交AD于M，交BC于N．
（1）求证：AM=CN；
（2）若∠CEN=90°，EN：AB=2：3，EC=3，求BC的长．

Answer 1

分析 （1）证明△AME≌△CNE，即可得出结论；
（2）证明△CEN∽△CBA，得出对应边成比例．即可求出BC的长．

解答 （1）证明：∵四边形ABCD是矩形，
∴AD∥BC，B=90°，
∴∠MAE=∠NCE，∠AME=∠CNE，
∵E是AC的中点，
∴AE=CE，
在△AME和△CNE中，$\left\{\begin{array}{l}{∠MAE=∠NCE}&{\;}\\{∠AME=∠CNE}&{\;}\\{AE=CE}&{\;}\end{array}\right.$，
∴△AME≌△CNE（AAS），
∴AM=CN；
（2）解：∵∠CEN=∠B=90°，∠ECN=∠BCA，
∴△CEN∽△CBA，
∴$\frac{CE}{CB}=\frac{EN}{AB}$=$\frac{2}{3}$，
即$\frac{3}{BC}=\frac{2}{3}$，
解得：BC=4.5．

点评 本题考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等和三角形相似是解决问题的关键．