题目内容
18.在△ABC中,∠C=90°,tanA=$\frac{2}{3}$,则sinA=( )| A. | $\frac{2\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | $\frac{3\sqrt{13}}{13}$ |
分析 根据正切函数的定义,勾股定理,可得AB的长,根据正弦函数的定义,可得答案.
解答 解:tanA=$\frac{BC}{AC}$=$\frac{2}{3}$,
设BC=2x,AC=3x,勾股定理,得
AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{13}$x,
sinA=$\frac{BC}{AB}$=$\frac{2x}{\sqrt{13}x}$=$\frac{2\sqrt{13}}{13}$,
故选:C.
点评 本题考查了同角三角函数关系,利用正切函数的定义,勾股定理得出AB的长是解题关键.

练习册系列答案
相关题目
9.一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为1980°,则原多边形的边数为( )
| A. | 11 | B. | 12 | C. | 13 | D. | 11或12 |
7.三角形的外心到三角形三个顶点的距离相等,它是三角形( )
| A. | 三个内角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三条中线的交点 |
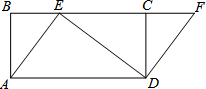 如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形. 小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.
小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米. 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.