题目内容
6. 小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.
小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.(1)求旗杆BC的高度;
(2)兴趣小组活动一段时间后,小明站在A,B两点之间的D处(A,D,B三点在一条直线上),测得旗杆BC的顶端C的仰角为α,且tanα=0.8,求此时小明与旗杆之间的距离.
分析 (1)根据相似三角形的性质可求旗杆BC的高度;
(2)在Rt△CFE中利用tan∠CEF求得EF的长,即可得到BD的长.
解答 解:(1)依题意有:
$\frac{AB}{BC}$=$\frac{2.4}{1.6}$,即$\frac{12}{BC}$=$\frac{2.4}{1.6}$, 解得BC=8.
解得BC=8.
故旗杆BC的高度是8米;
(2)如图,
在Rt△CFE中,tan∠CEF=$\frac{CF}{EF}$=$\frac{8-1.6}{EF}$=0.8,
解得EF=8,
则BD=8.
故此时小明与旗杆之间的距离是8米.
点评 此题主要考查了解直角三角形的应用-仰角俯角问题,解题的关键是从题目中整理出直角三角形并正确的利用边角关系求解.

练习册系列答案
相关题目
14.已知点A(4,0),B(0,3),如果⊙A的半径为1,⊙B的半径为6,则⊙A与⊙B的位置关系是( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
18.在△ABC中,∠C=90°,tanA=$\frac{2}{3}$,则sinA=( )
| A. | $\frac{2\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | $\frac{3\sqrt{13}}{13}$ |
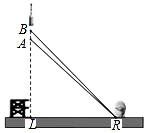 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.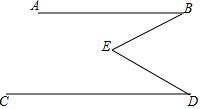 如图,已知∠BED=∠B+∠D,试说明AB∥CD.
如图,已知∠BED=∠B+∠D,试说明AB∥CD.
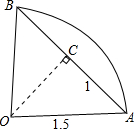 如图,某公路圆弧弯道半径OA为1.5km,弯道两端A,B的直线距离为2km,求:
如图,某公路圆弧弯道半径OA为1.5km,弯道两端A,B的直线距离为2km,求: