题目内容
10．先化简，再求值：（x-y）2-（x-y）（x+y）+（x+y）2，其中x=3，y=-$\frac{1}{3}$．分析 原式利用平方差公式，完全平方公式化简，去括号合并得到最简结果，把x与y的值代入计算即可求出值．
解答 解：原式=x-y2-x2+y2+x2+2xy+y2=x+2xy+y2，
当x=3，y=-$\frac{1}{3}$时，原式=3-2+$\frac{1}{9}$=1$\frac{1}{9}$．
点评 此题考查了整式的混合运算-化简求值，熟练掌握平方差公式，完全平方公式是解本题的关键．
练习册系列答案
相关题目
20．某校对九年级全部240名学生的血型作了调查，列出统计表，则该校九年级O型血的学生有36人．
| 组别 | A型 | B型 | AB型 | O 型 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
18．在△ABC中，∠C=90°，tanA=$\frac{2}{3}$，则sinA=（ ）
| A． | $\frac{2\sqrt{10}}{10}$ | B． | $\frac{3\sqrt{10}}{10}$ | C． | $\frac{2\sqrt{13}}{13}$ | D． | $\frac{3\sqrt{13}}{13}$ |
19．使$\sqrt{2x-10}$有意义的x的取值范围是（ ）
| A． | x＞5 | B． | x≥5 | C． | x≠5 | D． | 全体实数 |
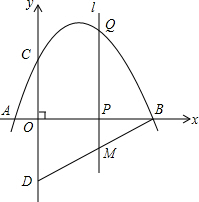如图，抛物线y=-$\frac{1}{3}$x2+$\frac{3}{2}$x+2与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．