题目内容
9.一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为1980°,则原多边形的边数为( )| A. | 11 | B. | 12 | C. | 13 | D. | 11或12 |
分析 根据多边形的内角和公式,可得答案.
解答 解:设新多边形为n边形,
(n-2)•180°=1980°,
解得n=13,
n-1=12.
故选:B.
点评 本题考查了多边形,多边形剪去一个角(剪痕不过任何一个其它顶点)边数增加1是解题关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.某校对九年级全部240名学生的血型作了调查,列出统计表,则该校九年级O型血的学生有36人.
| 组别 | A型 | B型 | AB型 | O 型 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
4.下列命题中,真命题是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 平分弦的直径垂直弦 | |
| C. | 有两边及一角对应相等的两个三角形全等 | |
| D. | 八边形的内角和是外角和的3倍 |
14.已知点A(4,0),B(0,3),如果⊙A的半径为1,⊙B的半径为6,则⊙A与⊙B的位置关系是( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
18.在△ABC中,∠C=90°,tanA=$\frac{2}{3}$,则sinA=( )
| A. | $\frac{2\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{13}}{13}$ | D. | $\frac{3\sqrt{13}}{13}$ |
19.使$\sqrt{2x-10}$有意义的x的取值范围是( )
| A. | x>5 | B. | x≥5 | C. | x≠5 | D. | 全体实数 |
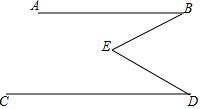 如图,已知∠BED=∠B+∠D,试说明AB∥CD.
如图,已知∠BED=∠B+∠D,试说明AB∥CD.