题目内容
1.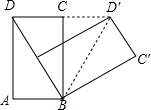 如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.
如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.
分析 根据旋转的性质得到∠CBD=∠C′BD′,BD=BD′,根据矩形的性质得到∠BCD=∠BCD′=90°,根据HL可证△BCD≌△BCD′,可得∠CBD=∠CBD′,进一步得到∠CBC′的度数.
解答 解:∵把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),
∴∠CBD=∠C′BD′,BD=BD′,∠BCD=∠BCD′=90°,
在Rt△BCD≌Rt△BCD′中,
$\left\{\begin{array}{l}{BC=BC}\\{BD=BD′}\end{array}\right.$
∴Rt△BCD≌Rt△BCD′(HL),
∴∠CBD=∠CBD′,
∴∠CBC′=90°×$\frac{2}{3}$=60°.
故∠CBC′的度数是60°.
点评 此题考查了矩形的性质,旋转的性质,解决本题的关键是弄清旋转前、后的图形全等.

练习册系列答案
相关题目
9.小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况:(单位:元)
根据上表回答问题:
(1)星期二收盘时,该股票每股多少元?
(2)一周内星期几该股票收盘时的赢利最多,星期几该股票收盘时的赢利最少,每股赢利分别是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌(元) | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
(1)星期二收盘时,该股票每股多少元?
(2)一周内星期几该股票收盘时的赢利最多,星期几该股票收盘时的赢利最少,每股赢利分别是多少?

 已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE.
已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE. 如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(-4,0),(-1,2),现将矩形ABCD向右平移2个单位后,再向上平移1个单位得到矩形EFGH.
如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(-4,0),(-1,2),现将矩形ABCD向右平移2个单位后,再向上平移1个单位得到矩形EFGH.