题目内容
13. 已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE.
已知:如图,在梯形ABCD中,∠C=∠D=90°,AD=m,BC=n,点E在CD上,且∠AEB=90°,AE=BE.(1)求梯形ABCD的面积(用含m、n的代数式表示).
(2)△ABE的面积$\frac{1}{2}$(m2+n2).(用含m、n的代数式表示).
分析 (1)先证明△BCE≌△EDA,推出BC=ED=n,AD=CE=m,CD=m+n,由此即可计算.
(2)构建勾股定理求出BE即可解决问题.
解答  解:(1)∵∠C=∠D=∠BEA=90°,
解:(1)∵∠C=∠D=∠BEA=90°,
∴∠CBE+∠CEB=90°,∠CEB+∠AED=90°,
∴∠CBE=∠AED,
在△BCE和△EDA中,
$\left\{\begin{array}{l}{∠C=∠D}\\{∠CBE=∠AED}\\{BE=AE}\end{array}\right.$,
∴△BCE≌△EDA,
∴BC=ED=n,AD=CE=m,CD=m+n,
∴梯形ADCB的面积=$\frac{1}{2}$(m+n)2,
(2)由(1)可知,BE=AE=$\sqrt{B{C}^{2}+E{C}^{2}}$=$\sqrt{{m}^{2}+{n}^{2}}$,
∴S△ABE=$\frac{1}{2}$BE•AE=$\frac{1}{2}$(m2+n2),
故答案为$\frac{1}{2}$(m2+n2).
点评 本题考查全等三角形的判定和性质,三角形的面积公式,梯形的面积公式,解题的关键是灵活意义这些知识解决问题,属于基础题中考常考题型.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
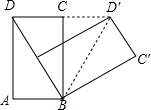 如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.
如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数. 如图,⊙O与△ABC各边分别切于点D,E,F,
如图,⊙O与△ABC各边分别切于点D,E,F,

 如图,已知E、F分别是△ABC的边AB和AC上的两个定点,在BC上找一点M,使△EFM的周长最小.(不写作法)
如图,已知E、F分别是△ABC的边AB和AC上的两个定点,在BC上找一点M,使△EFM的周长最小.(不写作法)