题目内容
10. 如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(-4,0),(-1,2),现将矩形ABCD向右平移2个单位后,再向上平移1个单位得到矩形EFGH.
如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(-4,0),(-1,2),现将矩形ABCD向右平移2个单位后,再向上平移1个单位得到矩形EFGH.(1)请求出点H的坐标.
(2)若将矩形ABCD与矩形EFGH理解为关于点P中心对称,请画出点P并求出点P的坐标.
分析 (1)先利用点平移的坐标规律得到E(-2,1)和点G的坐标为(1,3),然后利用矩形的性质可判断H点的横坐标与点E的横坐标相同,纵坐标与点G的纵坐标相同,从而得到H点的坐标;
(2)连接两组对应点即可得到点P,然后根据矩形的性质和线段的中点坐标公式可确定P点坐标.
解答 解:(1)∵点A(-4,0)向右平移2个单位后,再向上平移1个单位得到点E,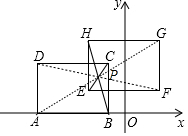
∴点E的坐标为(-2,1),
∵点C(-1,2)向右平移2个单位后,再向上平移1个单位得到点G,
∴点G的坐标为(1,3),
∴H点的坐标为(-2,3);
(2)连接BH、CE,它们的交点为点P,如图,
P点坐标为(-1.5,1.5).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移的性质和矩形的性质.

练习册系列答案
相关题目
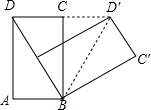 如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.
如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.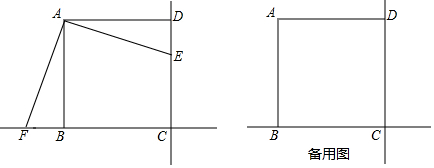


 如图,已知E、F分别是△ABC的边AB和AC上的两个定点,在BC上找一点M,使△EFM的周长最小.(不写作法)
如图,已知E、F分别是△ABC的边AB和AC上的两个定点,在BC上找一点M,使△EFM的周长最小.(不写作法) 如图所示,AE是△ABC的角平分线,AD⊥BC于点D.
如图所示,AE是△ABC的角平分线,AD⊥BC于点D.