题目内容
 已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.
已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.考点:全等三角形的判定与性质,平行线的判定与性质
专题:证明题
分析:由∠B+∠BCF=180°,利用同旁内角互补两直线平行,得到AB与CF平行,利用两直线平行得到两对内错角相等,再由E为DF的中点,利用AAS得到三角形ADE与三角形CFE全等,利用全等三角形的对应边相等可得出AE=CE.
解答:证明:∵∠B+∠BCF=180°,
∴AB∥CF,
∴∠A=∠ECF,∠ADE=∠F,
又E为DF的中点,
∴DE=FE,
在△ADE和△CFE中,
∵
,
∴△ADE≌△CFE(AAS),
∴AE=CE.
∴AB∥CF,
∴∠A=∠ECF,∠ADE=∠F,
又E为DF的中点,
∴DE=FE,
在△ADE和△CFE中,
∵
|
∴△ADE≌△CFE(AAS),
∴AE=CE.
点评:此题考查了全等三角形的判定与性质,以及平行线的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中正确的结论是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中正确的结论是( )| A、abc>0 |
| B、a+b>m(am+b),(m为实数且m≠1) |
| C、b<a+c |
| D、2a-b=0 |
 如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC=
如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC= 已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.
已知△ABC中,AB=AC,以AB为直径的⊙O1分别交AC、BC于两D、E点,过B点的切线交OE的延长线于点F,连FD、BD、OD,下列结论:①四边形ODCE是平行四边形;②E是△BFD的内心;③E是△FDO的外心;④∠C=∠BFD;其中正确的有( )个.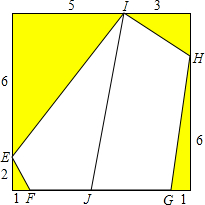 在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是
在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是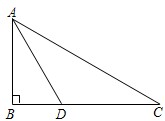 如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,
如图,某中学九年级数学兴趣小组测量校内旗杆AB高度,在C点测得旗杆顶端A的仰角为30°,向前走了26米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度忽略不计,点B、D、C在同一直线上),求旗杆AB的高度(结果保留3个有效数字,