题目内容
 如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC=
如图,AB是⊙O直径,AC是弦,OD⊥CB于点D,若OD=3,则AC=考点:圆周角定理,三角形中位线定理,垂径定理
专题:
分析:由OD⊥CB,根据垂径定理的即可求得,CD=BD,又由OA=OB,可得OD是△ABC的中位线,根据三角形中位线的性质,即可求得答案.
解答:解:∵OD⊥CB,
∴CD=BD,
∵AB是⊙O直径,
∴OA=OB,
∴AC=2OD=2×3=6.
故答案为:6.
∴CD=BD,
∵AB是⊙O直径,
∴OA=OB,
∴AC=2OD=2×3=6.
故答案为:6.
点评:此题考查了垂径定理与三角形中位线的性质.此题难度不大,注意数形结合思想的应用.

练习册系列答案
相关题目
菱形的两条对角线长分别为6cm,8cm,则这个菱形的周长是( )
| A、14cm | B、20cm |
| C、32cm | D、48cm |
若数n=
,则数n3中含有数字9的个数是( )
| ||
| 20个9 |
| A、39 | B、37 | C、34 | D、31 |
下列函数关系中,不属于二次函数的是( )
| A、y=1-x2 |
| B、y=(3x+2)(4x-3)-12x2 |
| C、y=ax2+bx+c(a≠0) |
| D、y=(x-2)2+2 |
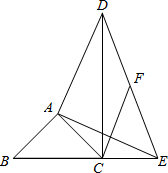 已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE. 已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.
已知:如图,D是△ABC的边AB上一点,∠B+∠BCF=180°,DF交AC于点E,点E为DF中点.求证:AE=CE.